Revision history for BP981
|
|
| Displaying 1-25 of 101 results found.
|
page 1 2 3 4 5
|
|
|
Edits shown per page: 25.
|
|
|
|
|
|
| |
| |
| |
|
| | |
|
|
|
-DATA
|
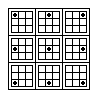 EX10090 |
| |
|
|
| |
| |
| |
|
| | |
|
|
|
REMOVE
|
 EX9996 |
| |
|
|
| |
| |
| |
|
| | |
|
|
|
-DATA
|
 EX10018 |
| |
|
|
| |
| |
| |
|
| | |
|
|
|
-DATA
|
 EX10019 |
| |
|
|
| |
| |
| |
|
| | |
|
|
|
COMMENTS
|
On the left, each row and column could be labeled by a certain object or concept; on the right this is not so.
More specifically: on the left, each row and each column is associated with a certain object or concept; there is a rule for combining rows and columns to give images; it would be possible without changing the rule to extend with new rows/columns or delete/reorder any existing columns. On the right, this is not so; the rule might be about how the images must relate to their neighbors, for example.
All examples show grids of squares with an image in each square, such that there is some "rule" the images within the grid obey.
Left examples are a generalized version of the analogy grids seen in BP361. Any analogy a : b :: c : d shown in a 2x2 grid will fit on the left here.
To word the solution with mathematical jargon, "defines a (simply described) map from the Cartesian product of two sets vs. not so." Another equivalent solution is "columns (alternatively, rows) illustrate a consistent set of one-input operations." It is always possible to imagine the columns as inputs and the rows as operations and vice versa.
There is a trivial way in which any example can be interpreted so that it fits on the left side: imagine each row is assigned the list of all the squares in that row and each column is assigned its number, counting from the left. But each grid has a clear rule that is simpler than this. |
| |
|
|
| |
| |
| |
|
| | |
|
|
|
COMMENTS
|
On the left, each row and column could be labeled by a certain object or concept; on the right this is not so.
More specifically: on the left, each row and each column is associated with a certain object or concept; there is a rule for combining rows and columns to give images; it would be possible to extend with new rows/columns or delete/reorder any existing columns. On the right, this is not so; the rule might be about how the images must relate to their neighbors, for example.
All examples show grids of squares with an image in each square, such that there is some "rule" the images within the grid obey.
Left examples are a generalized version of the analogy grids seen in BP361. Any analogy a : b :: c : d shown in a 2x2 grid will fit on the left here.
To word the solution with mathematical jargon, "defines a (simply described) map from the Cartesian product of two sets vs. not so." Another equivalent solution is "columns (alternatively, rows) illustrate a consistent set of one-input operations." It is always possible to imagine the columns as inputs and the rows as operations and vice versa.
There is a trivial way in which any example can be interpreted so that it fits on the left side: imagine each row is assigned the list of all the squares in that row and each column is assigned its number, counting from the left. But each grid has a clear rule that is simpler than this. |
| |
|
|
| |
| |
| |
|
| | |
|
|
|
CROSSREFS
|
BP1258 is a similar idea: "any square removed could be reconstructed vs. not." Examples included left here usually fit left there, but some do not e.g. EX9998.
See BP979 for use of similar structures but with one square removed from the grid. |
| |
|
|
| |
| |
| |
|
| | |
|
|
|
CROSSREFS
|
BP1258 is a similar idea: "any square removed could be reconstructed vs. not." Examples included left here usually fit left there, but some do not e.g. EX9998. Plenty of examples on the right here fit left there.
See BP979 for use of similar structures but with one square removed from the grid. |
| |
|
|
| |
| |
| |
|
| | |
|
|
|
CROSSREFS
|
BP1258 is a similar idea: "any square removed could be reconstructed based on the rule vs. not." Examples included left here usually fit left there, but some do not e.g. EX9998. Plenty of examples on the right here fit left there.
See BP979 for use of similar structures but with one square removed from the grid. |
| |
|
|
| |
| |
| |
|
| | |
|
|
|
CROSSREFS
|
BP1258 is a similar idea that does not quite work as a solution here: "any square removed could be reconstructed vs. not." Examples included left here usually fit left there, but some do not e.g. EX9998.
See BP979 for use of similar structures but with one square removed from the grid. |
| |
|
|
| |
| |
| |
|
| | |
|
|
|
CROSSREFS
|
BP1258 is a similar idea that does not quite work as a solution here: "any square removed could be reconstructed based on the rule vs. not." Examples included left here usually fit left there, but some do not e.g. EX9998.
See BP979 for use of similar structures but with one square removed from the grid. |
| |
|
|
| |
| |
| |
|
| | |
|
|
|
CROSSREFS
|
BP1258 is a similar idea that does not quite work as a solution here: "any square removed could be reconstructed based on the rule vs. not." All of the examples included left here fit left there.
See BP979 for use of similar structures but with one square removed from the grid. |
| |
|
|
| |
| |
| |
|
| | |
|
|
|
CROSSREFS
|
See BP979 for use of similar structures but with one square removed from the grid. Examples on the left here with any square removed should fit on the left there.
BP1258 is a similar idea that does not quite work as a solution here: "any square removed could be reconstructed based on the rule vs. not." |
| |
|
|
| |
| |
| |
|
| | |
|
|
|
COMMENTS
|
On the left, each row and column could be "labeled" by a certain object or concept; on the right this is not so.
More specifically: on the left, each row and each column is associated with a certain object or concept; there is a rule for combining rows and columns to give images; it would be possible to extend with new rows/columns or delete/reorder any existing columns. On the right, this is not so; the rule might be about how the images must relate to their neighbors, for example.
All examples show grids of squares with an image in each square, such that there is some "rule" the images within the grid obey.
Left examples are a generalized version of the analogy grids seen in BP361. Any analogy a : b :: c : d shown in a 2x2 grid will fit on the left here.
To word the solution with mathematical jargon, "defines a (simply described) map from the Cartesian product of two sets vs. not so." Another equivalent solution is "columns (alternatively, rows) illustrate a consistent set of one-input operations." It is always possible to imagine the columns as inputs and the rows as operations and vice versa.
There is a trivial way in which any example can be interpreted so that it fits on the left side: imagine each row is assigned the list of all the squares in that row and each column is assigned its number, counting from the left. But each grid has a clear rule that is simpler than this. |
| |
|
|
| |
| |
| |
|
| | |
|
|
|
COMMENTS
|
On the left, each row and column could be "labeled" by a certain object or concept; on the right this is not so.
More specifically: on the left, each row and each column is associated with a certain object or concept; there is a rule for combining rows and columns to give images; it would be possible to extend with new rows/columns or delete/reorder any existing columns. On the right, this is not so; the rule might be about how the images must relate to their neighbors, for example.
All examples show grids of squares with an image in each square, such that there is some "rule" the images within the grid obey.
Left examples are a generalized version of the analogy grids seen in BP361. Any analogy a : b :: c : d shown in a 2x2 grid will fit on the left here.
To word the solution with mathematical jargon, "defines a (simply described) map from the Cartesian product of two sets vs. not so." Another equivalent solution is "columns (alternatively, rows) illustrate a consistent set of one-input operations." It is always possible to imagine the columns as inputs and the rows as operations and vice versa.
Similar idea that does not quite work as a solution here: any removed square could be reconstructed based on the rule vs. not.
There is a trivial way in which any example can be interpreted so that it fits on the left side: imagine each row is assigned the list of all the squares in that row and each column is assigned its number, counting from the left. But each grid has a clear rule that is simpler than this. |
| |
|
|
| |
| |
| |
|
| | |
|
|
|
REMOVE
|
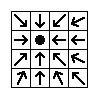 EX10002 |
| |
|
|
| |
| |
| |
|
| | |
|
|
|
REMOVE
|
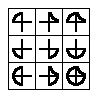 EX10040 |
| |
|
|
| |
| |
| |
|
| | |
|
|
|
-DATA
|
 EX10040 |
| |
|
|
| |
| |
| |
|
| | |
|
|
|
-DATA
|
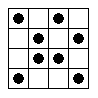 EX10020 |
| |
|
|
| |
| |
| |
|
| | |
|
|
|
COMMENTS
|
All examples show grids of squares with an image in each square, such that there is some "rule" the images within the grid obey.
On the left, each row and each column is associated with a certain object or concept; there is a rule for combining rows and columns to give images; it would be possible to extend with new rows/columns or delete/reorder any existing columns.
On the right, this is not so. The rule might be about how the images must relate to their neighbors, for example.
Left examples are a generalized version of the analogy grids seen in BP361. Any analogy a : b :: c : d shown in a 2x2 grid will fit on the left here.
To word the solution with mathematical jargon, "defines a (simply described) map from the Cartesian product of two sets vs. not so." Another equivalent solution is "columns (alternatively, rows) illustrate a consistent set of one-input operations." It is always possible to imagine the columns as inputs and the rows as operations and vice versa.
Similar idea that does not quite work as a solution here: any removed square could be reconstructed based on the rule vs. not.
There is a trivial way in which any example can be interpreted so that it fits on the left side: imagine each row is assigned the list of all the squares in that row and each column is assigned its number, counting from the left. But each grid has a clear rule that is simpler than this. |
| |
|
|
| |
| |
| |
|
| | |
|
|
|
COMMENTS
|
All examples show grids of squares with an image in each square, such that there is some "rule" the images within the grid obey.
On the left, each row and each column is associated with a certain object or concept; there is a rule for combining rows and columns to give images; it would be possible to extend with new rows/columns or delete/reorder any existing columns.
On the right, the "rule" might be about how the images must relate to their neighbors, for example.
Left examples are a generalized version of the analogy grids seen in BP361. Any analogy a : b :: c : d shown in a 2x2 grid will fit on the left here.
To word the solution with mathematical jargon, "defines a (simply described) map from the Cartesian product of two sets vs. not so." Another equivalent solution is "columns (alternatively, rows) illustrate a consistent set of one-input operations." It is always possible to imagine the columns as inputs and the rows as operations and vice versa.
Similar idea that does not quite work as a solution here: any removed square could be reconstructed based on the rule vs. not.
There is a trivial way in which any example can be interpreted so that it fits on the left side: imagine each row is assigned the list of all the squares in that row and each column is assigned its number, counting from the left. But each grid has a clear rule that is simpler than this. |
| |
|
|
| |
| |
| |
|
| | |
|
|
|
COMMENTS
|
Left examples are a generalized version of the analogy grids seen in BP361. Any analogy a : b :: c : d shown in a 2x2 grid will fit on the left here.
Each row and each column is associated with a certain object or concept; there is a rule for combining rows and columns to give images; it would be possible to extend with new rows/columns or delete/reorder any existing columns.
All examples show grids of squares with an image in each square, such that there is some "rule" the images within the grid obey. The "rule" might be about how the images must relate to their neighbors, for example.
To word the solution with mathematical jargon, "defines a (simply described) map from the Cartesian product of two sets vs. not so." Another equivalent solution is "columns (alternatively, rows) illustrate a consistent set of one-input operations." It is always possible to imagine the columns as inputs and the rows as operations and vice versa.
Similar idea that does not quite work as a solution here: any removed square could be reconstructed based on the rule vs. not.
There is a trivial way in which any example can be interpreted so that it fits on the left side: imagine each row is assigned the list of all the squares in that row and each column is assigned its number, counting from the left. But each grid has a clear rule that is simpler than this. |
| |
|
|
| |
| |
| |
|
| | |
|
|
|
COMMENTS
|
Left examples are a generalized version of the analogy grids seen in BP361. Any analogy a : b :: c : d shown in a 2x2 grid will fit on the left here.
More specifically:
Each row and each column is associated with a certain object or concept; there is a rule for combining rows and columns to give images. It would be possible to extend with new rows/columns or delete/reorder any existing columns.
All examples show grids of squares with an image in each square, such that there is some "rule" the images within the grid obey. The "rule" might be about how the images must relate to their neighbors, for example.
To word the solution with mathematical jargon, "defines a (simply described) map from the Cartesian product of two sets vs. not so." Another equivalent solution is "columns (alternatively, rows) illustrate a consistent set of one-input operations." It is always possible to imagine the columns as inputs and the rows as operations and vice versa.
Similar idea that does not quite work as a solution here: any removed square could be reconstructed based on the rule vs. not.
There is a trivial way in which any example can be interpreted so that it fits on the left side: imagine each row is assigned the list of all the squares in that row and each column is assigned its number, counting from the left. But each grid has a clear rule that is simpler than this. |
| |
|
|
| |
| |
| |
|
| | |
|
|
|
+DATA
|
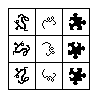 EX10003 |
| |
|
|
| |
| |
| |
|
| | |
|
|
|
COMMENTS
|
Left examples are a generalized version of the analogy grids seen in BP361. Any analogy a : b :: c : d shown in a 2x2 grid will fit on the left of here.
More specifically:
Each row and each column is associated with a certain object or concept; there is a rule for combining rows and columns to give images. It would be possible to extend with new rows/columns or delete/reorder any existing columns.
All examples show grids of squares with an image in each square, such that there is some "rule" the images within the grid obey. The "rule" might be about how the images must relate to their neighbors, for example.
To word the solution with mathematical jargon, "defines a (simply described) map from the Cartesian product of two sets vs. not so." Another equivalent solution is "columns (alternatively, rows) illustrate a consistent set of one-input operations." It is always possible to imagine the columns as inputs and the rows as operations and vice versa.
Similar idea that does not quite work as a solution here: any removed square could be reconstructed based on the rule vs. not.
There is a trivial way in which any example can be interpreted so that it fits on the left side: imagine each row is assigned the list of all the squares in that row and each column is assigned its number, counting from the left. But each grid has a clear rule that is simpler than this. |
| |
|
|