Revision history for BP981
|
|
| Displaying 51-75 of 101 results found.
|
page 1 2 3 4 5
|
|
|
Edits shown per page: 25.
|
|
|
|
|
|
| |
| |
| |
|
| | |
|
|
|
COMMENTS
|
Left examples are a generalized version of the analogy grids seen in BP361. Any analogy a : b :: c : d shown in a 2x2 grid will fit on the left of this Problem.
All examples show grids of squares with an image in each square, such that there is some "rule" the images within the grid obey. The "rule" might be about how the images must relate to their neighbors, for example.
To word the solution with mathematical jargon, "defines a (simply described) map from the Cartesian product of two sets vs. not so." Another equivalent solution is "columns (alternatively, rows) illustrate a consistent set of one-input operations." It is always possible to imagine the columns as inputs and the rows as operations and vice versa.
Similar idea that does not quite work as a solution here: any removed square could be reconstructed based on the rule vs. not.
There is a trivial way in which any example can be interpreted so that it fits on the left side: imagine each row is assigned the list of all the squares in that row and each column is assigned its number, counting from the left. But each grid has a clear rule that is simpler than this. |
| |
|
|
| |
| |
| |
|
| | |
|
|
|
COMMENTS
|
To word the solution with mathematical jargon, "defines a (simply described) map from the Cartesian product of two sets vs. not so." Another equivalent solution is "columns (alternatively, rows) illustrate a consistent set of one-input operations." It is always possible to imagine the columns as inputs and the rows as operations and vice versa.
Left examples are a generalized version of the analogy grids seen in BP361. Any analogy a : b :: c : d shown in a 2x2 grid will fit on the left of this Problem.
Similar idea that does not quite work as a solution here: any removed square could be reconstructed based on the rule vs. not.
All examples show grids of squares with an image in each square, such that there is some "rule" the images within the grid obey. The "rule" might be about how the images must relate to their neighbors, for example.
There is a trivial way in which any example can be interpreted so that it fits on the left side: imagine each row is assigned the list of all the squares in that row and each column is assigned its number, counting from the left. But each grid has a clear rule that is simpler than this. |
| |
|
|
| |
| |
| |
|
| | |
|
|
|
COMMENTS
|
Similar idea that does not quite work as a solution: any removed square could be reconstructed based on the rule vs. not.
To word the solution with mathematical jargon, "defines a (simply described) map from the Cartesian product of two sets vs. not so." Another equivalent solution is "columns (alternatively, rows) illustrate a consistent set of one-input operations." It is always possible to imagine the columns as inputs and the rows as operations and vice versa.
Left examples are a generalized version of the analogy grids seen in BP361. Any analogy a : b :: c : d shown in a 2x2 grid will fit on the left of this Problem.
All examples show grids of squares with an image in each square, such that there is some "rule" the images within the grid obey. The "rule" might be about how the images must relate to their neighbors, for example.
There is a trivial way in which any example can be interpreted so that it fits on the left side: imagine each row is assigned the list of all the squares in that row and each column is assigned its number, counting from the left. But each grid has a clear rule that is simpler than this. |
| |
|
|
| |
| |
| |
|
| | |
|
|
|
COMMENTS
|
Alternative solution: any square removed could be reconstructed based on the rule vs. not.
To word the solution with mathematical jargon, "defines a (simply described) map from the Cartesian product of two sets vs. not so." Another equivalent solution is "columns (alternatively, rows) illustrate a consistent set of one-input operations." It is always possible to imagine the columns as inputs and the rows as operations and vice versa.
Left examples are a generalized version of the analogy grids seen in BP361. Any analogy a : b :: c : d shown in a 2x2 grid will fit on the left of this Problem.
All examples show grids of squares with an image in each square, such that there is some "rule" the images within the grid obey. The "rule" might be about how the images must relate to their neighbors, for example.
There is a trivial way in which any example can be interpreted so that it fits on the left side: imagine each row is assigned the list of all the squares in that row and each column is assigned its number, counting from the left. But each grid has a clear rule that is simpler than this. |
| |
|
|
| |
| |
| |
|
| | |
|
|
|
COMMENTS
|
Alternative solution: any square removed could be reconstructed vs. not.
To word the solution with mathematical jargon, "defines a (simply described) map from the Cartesian product of two sets vs. not so." Another equivalent solution is "columns (alternatively, rows) illustrate a consistent set of one-input operations." It is always possible to imagine the columns as inputs and the rows as operations and vice versa.
Left examples are a generalized version of the analogy grids seen in BP361. Any analogy a : b :: c : d shown in a 2x2 grid will fit on the left of this Problem.
All examples show grids of squares with an image in each square, such that there is some "rule" the images within the grid obey. The "rule" might be about how the images must relate to their neighbors, for example.
There is a trivial way in which any example can be interpreted so that it fits on the left side: imagine each row is assigned the list of all the squares in that row and each column is assigned its number, counting from the left. But each grid has a clear rule that is simpler than this. |
| |
|
|
| |
| |
| |
|
| | |
|
|
|
+DATA
|
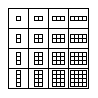 EX9993 |
| |
|
|
| |
| |
| |
|
| | |
|
|
|
COMMENTS
|
Example: on the left is an image of a grid where the first row features a square with three dots and a square with nine dots, and the second row features a square with four dots and square with sixteen dots. "Three" and "four" are assigned to the rows; "x" and "x squared" are assigned to the columns.
To word the solution with mathematical jargon, "defines a (simply described) map from the Cartesian product of two sets vs. not so." Another equivalent solution is "columns (alternatively, rows) illustrate a consistent set of one-input operations." It is always possible to imagine the columns as inputs and the rows as operations and vice versa.
Left examples are a generalized version of the analogy grids seen in BP361. Any analogy a : b :: c : d shown in a 2x2 grid will fit on the left of this Problem.
All examples show grids of squares with an image in each square, such that there is some "rule" the images within the grid obey. The "rule" might be about how the images must relate to their neighbors, for example.
There is a trivial way in which any example can be interpreted so that it fits on the left side: imagine each row is assigned the list of all the squares in that row and each column is assigned its number, counting from the left. But each grid has a clear rule that is simpler than this. |
| |
|
|
| |
| |
| |
|
| | |
|
|
|
CROSSREFS
|
See BP979 for use of similar structures but with one square removed from the grid. Examples on the left here with any square removed should fit on the left there. |
| |
|
|
| |
| |
| |
|
| | |
|
|
|
REMOVE
|
 EX8116 |
| |
|
|
| |
| |
| |
|
| | |
|
|
|
COMMENTS
|
To clarify the solution with an example: on the left is an image of a grid where the first row features a square with three dots and a square with nine dots, and the second row features a square with four dots and square with sixteen dots. "Three" and "four" are assigned to the rows; "x" and "x squared" are assigned to the columns.
To word the solution with mathematical jargon, "defines a (simply described) map from the Cartesian product of two sets vs. not so." Another equivalent solution is "columns (alternatively, rows) illustrate a consistent set of one-input operations." It is always possible to imagine the columns as inputs and the rows as operations and vice versa.
Left examples are a generalized version of the analogy grids seen in BP361. Any analogy a : b :: c : d shown in a 2x2 grid will fit on the left of this Problem.
All examples show grids of squares with an image in each square, such that there is some "rule" the images within the grid obey. The "rule" might be about how the images must relate to their neighbors, for example.
There is a trivial way in which any example can be interpreted so that it fits on the left side: imagine each row is assigned the list of all the squares in that row and each column is assigned its number, counting from the left. But each grid has a clear rule that is simpler than this. |
| |
|
|
| |
| |
| |
|
| | |
|
|
|
NAME
|
Each column is assigned something independently; each row is assigned something independently; there is a rule that generates contents of squares from the row information and column information vs. there is a different kind of rule.
|
| |
|
|
| |
| |
| |
|
| | |
|
|
|
NAME
|
Each column is assigned something independently; each row is assigned something independently; there is a rule that generates the contents of squares from the row's information and column's information vs. there is a different kind of rule.
|
| |
|
|
| |
| |
| |
|
| | |
|
|
|
COMMENTS
|
To clarify the solution with an example: on the left is an image of a grid where the first row features a square with three dots and a square with nine dots, and the second row features a square with four dots and square with sixteen dots. "Three" and "four" are assigned to the rows; "x" and "x squared" are assigned to the columns.
To word the solution with mathematical jargon, "defines a (simply described) map from the Cartesian product of two sets vs. not so." Another equivalent solution is "columns (or rows) illustrate a consistent set of one-input operations." It is always possible to imagine the columns as inputs and the rows as operations and vice versa.
Left examples are a generalized version of the analogy grids seen in BP361. Any analogy a : b :: c : d shown in a 2x2 grid will fit on the left of this Problem.
All examples show grids of squares with an image in each square, such that there is some "rule" the images within the grid obey. The "rule" might be about how the images must relate to their neighbors, for example.
There is a trivial way in which any example can be interpreted so that it fits on the left side: imagine each row is assigned the list of all the squares in that row and each column is assigned its number, counting from the left. But each grid has a clear rule that is simpler than this. |
| |
|
|
| |
| |
| |
|
| | |
|
|
|
NAME
|
Each column is assigned something; each row is assigned something; there is a rule that generates the contents of squares from the row's information and column's information vs. not so.
|
| |
|
|
| |
| |
| |
|
| | |
|
|
|
COMMENTS
|
To clarify the solution with an example: on the left is an image of a grid where the first row features a square with three dots and a square with nine dots, and the second row features a square with four dots and square with sixteen dots. "Three" and "four" are assigned to the rows; "x" and "x squared" are assigned to the columns.
An equivalent solution with more mathematical jargon is "defines (an intuitive) map from the Cartesian product of two sets vs. not so." Another equivalent solution is "columns (or rows) illustrate a consistent set of one-input operations." It is always possible to imagine the columns as inputs and the rows as operations and vice versa.
Left examples are a generalized version of the analogy structures seen in BP361. Any analogy a : b :: c : d shown in a 2x2 grid will fit on the left of this Problem.
With many more examples this BP could be used to nonverbally teach this structure to somebody. (This is the keyword "teach", left-BP858.)
All examples show grids of squares with an image in each square, such that there is some "rule" the images within the grid obey. The "rule" can be about how the images relate to their neighbors, it can involve the position of the images in the grid, and it can involve properties of the grid considered as a whole.
There is a trivial way in which any example can be interpreted so that it fits on the left side: imagine each row is assigned the list of all the squares in that row and each column is assigned its number counting from the left. Then the rows and columns will indeed combine in a natural way to give the images shown. As such, all grids in this Problem should show a rule that is more intuitive than "assign each row the list of all the squares in it and each column its number counting from the left and let a square in the grid show the square at that place in the corresponding list". |
| |
|
|
| |
| |
| |
|
| | |
|
|
|
NAME
|
To each column is assigned something; to each row is assigned something; columns and rows combine via a consistent rule vs. not so.
|
|
|
COMMENTS
|
To clarify the solution with an example: on the left is an image of a grid where the first row features a square with three dots and a square with nine dots, and the second row features a square with four dots and square with sixteen dots. "Three" and "four" are assigned to the rows; "x" and "x squared" are assigned to the columns.
An equivalent solution with more mathematical jargon is "defines (an intuitive) map from the Cartesian product of two sets vs. not so." Another equivalent solution is "columns (or rows) illustrate a consistent set of one-input operations." It is always possible to imagine the columns as inputs and the rows as operations and vice versa.
Left examples are a generalized version of the analogy structures seen in BP361. Any analogy a : b :: c : d shown in a 2x2 grid will fit on the left of this Problem.
With many more examples this BP could be used to nonverbally teach this structure to somebody. (This is the keyword "teach", left-BP858.)
All examples show grids of squares with an image in each square, such that there is some "rule" the images within the grid obey. The "rule" can be about how the images relate to their neighbors, it can involve the position of the images in the grid, and it can involve properties of the grid considered as a whole.
There is a trivial way in which any example can be parsed so that it fits on the left side: imagine each row is assigned the list of all the squares in that row and each column is assigned its number counting from the left. Then the rows and columns will indeed combine in a natural way to give the images shown. As such, all grids in this Problem should show a rule that is more intuitive to parse than "assign each row the list of all the squares in it and each column its number counting from the left and let a square in the grid show the square at that place in the corresponding list". |
| |
|
|
| |
| |
| |
|
| | |
|
|
|
COMMENTS
|
To clarify the solution with an example: on the left is an image of a grid where the first row features a square with three dots and a square with nine dots, and the second row features a square with four dots and square with sixteen dots. "Three" and "four" are assigned to the rows; "x" and "x squared" are assigned to the columns.
An equivalent solution with more mathematical jargon is "defines (an intuitive) map from the Cartesian product of two sets vs. not so." Another equivalent solution is "columns (or rows) illustrate a consistent set of one-input operations." It is always possible to imagine the columns as inputs and the rows as operations and vice versa.
Left examples are a generalized version of the analogy structures seen in BP361. Any analogy a : b :: c : d shown in a 2x2 grid will fit on the left of this Problem.
With many more examples this BP could be used to nonverbally teach this structure to somebody. (This is the keyword "teach", left-BP858.)
All examples show grids of squares with an image in each square, such that there is some "rule" the images within the grid obey. The "rule" can be about how the images relate to their neighbors, it can involve the position of the images in the grid, and it can involve properties of the grid considered as a whole.
There is a trivial way in which any example can be parsed so that it fits on the left side: imagine each row is assigned the list of all the squares in that row and each column is assigned its number counting from the left. Then the rows and columns will indeed combine in a natural way to give the images shown. As such, all grids in this Problem should show a rule that is more intuitive to parse than "assign each row the list of all the squares in it and each column its number counting from the left and let a square in the grid show the respective square assigned at that place in the corresponding row". |
| |
|
|
| |
| |
| |
|
| | |
|
|
|
COMMENTS
|
To clarify the solution with an example: on the left is an image of a grid where the first row features a square with three dots and a square with nine dots, and the second row features a square with four dots and square with sixteen dots. "Three" and "four" are assigned to the rows; "x" and "x squared" are assigned to the columns.
An equivalent solution with more mathematical jargon is "defines (an intuitive) map from the Cartesian product of two sets vs. not so." Another equivalent solution is "columns (or rows) illustrate a consistent set of one-input operations." It is always possible to imagine the columns as inputs and the rows as operations and vice versa.
Left examples are a generalized version of the analogy structures seen in BP361. Any visual analogy a : b :: c : d shown in a 2x2 grid will fit on the left of this Problem.
With many more examples this BP could be used to nonverbally teach this structure to somebody. (This is the keyword "teach", left-BP858.)
All examples show grids of squares with an image in each square, such that there is some "rule" the images within the grid obey. The "rule" can be about how the images relate to their neighbors, it can involve the position of the images in the grid, and it can involve properties of the grid considered as a whole.
There is a trivial way in which any example can be parsed so that it fits on the left side: imagine each row is assigned the list of all the squares in that row and each column is assigned its number counting from the left. Then the rows and columns will indeed combine in a natural way to give the images shown. As such, all grids in this Problem should show a rule that is more intuitive to parse than "assign each row the list of all the squares in it and each column its number counting from the left and let a square in the grid show the respective square assigned at that place in the corresponding row". |
| |
|
|
| |
| |
| |
|
| | |
|
|
|
COMMENTS
|
To clarify the solution with an example: on the left is an image of a grid where the first row features a square with three dots and a square with nine dots, and the second row features a square with four dots and square with sixteen dots. "Three" and "four" are assigned to the rows; "x" and "x squared" are assigned to the columns.
An equivalent solution with more mathematical jargon is "defines (an intuitive) map from the Cartesian product of two sets vs. not so." Another equivalent solution is "columns (or rows) illustrate a consistent set of one-input operations." It is always possible to imagine the columns as inputs and the rows as operations and vice versa.
Left examples are a generalized version of the analogy structures seen in BP361. Any typical visual analogy a : b :: c : d shown in a 2x2 grid will fit on the left of this Problem.
This is a "teach" Problem (left-BP858); with many more examples it could be used to nonverbally teach this structure to somebody, similarly to BP968.
All examples show grids of squares with an image in each square, such that there is some "rule" the images within the grid obey. The "rule" can be about how the images relate to their neighbors, it can involve the position of the images in the grid, and it can involve properties of the grid considered as a whole.
There is a trivial way in which any example can be parsed so that it fits on the left side: imagine each row is assigned the list of all the squares in that row and each column is assigned its number counting from the left. Then the rows and columns will indeed combine in a natural way to give the images shown. As such, all grids in this Problem should show a rule that is more intuitive to parse than "assign each row the list of all the squares in it and each column its number counting from the left and let a square in the grid show the respective square assigned at that place in the corresponding row". |
| |
|
|
| |
| |
| |
|
| | |
|
|
|
COMMENTS
|
To clarify the solution with an example: on the left is an image of a grid where the first row features a square with three dots and a square with nine dots, and the second row features a square with four dots and square with sixteen dots. "Three" and "four" are assigned to the rows; "x" and "x squared" are assigned to the columns.
An equivalent solution with more mathematical jargon is "defines (an intuitive) map from the Cartesian product of two sets vs. not so." Another equivalent solution is "columns (or rows) illustrate a consistent set of one-input operations." It is always possible to imagine the columns as inputs and the rows as operations and vice versa.
Left examples are a generalized version of the analogy structures seen in BP361. Any typical visual analogy a : b :: c : d shown in a 2x2 grid will fit on the left of this Problem.
This is a "teach" Problem (left-BP858); with many more examples it could be used to nonverbally teach this structure to somebody, similarly to BP968.
All examples show grids of squares with an image in each square, such that there is some "rule" the images within the grid obey. The "rule" can be about how the images relate to their neighbors, it can involve the position of the images in the grid, and it can involve properties of the grid considered as a whole.
There is a trivial way in which any example can be parsed so that it fits on the left side: imagine each row is assigned the list of all the squares in that row and each column is assigned its number counting from the left. Then the rows and columns will indeed combine in a natural way to give the images shown. As such, the solution of this Problem assumes use of more natural interpretations of rules for these grids. All grids in this Problem should show a rule that is more intuitive to parse than "assign each row the list of all the squares in it and each column its number counting from the left and let a square in the grid show the respective square assigned at that place in the corresponding row." (Even just a random choice of squares is probably more intuitive than that, so one might say it is impossible for that to be the most intuitive rule.) |
|
|
EXAMPLE
|
|
| |
|
|
| |
| |
| |
|
| | |
|
|
|
COMMENTS
|
To clarify the solution with an example: on the left is an image of a grid where the first row features a square with three dots and a square with nine dots, and the second row features a square with four dots and square with sixteen dots. "Three" and "four" are assigned to the rows; "x" and "x squared" are assigned to the columns.
An equivalent solution with more mathematical jargon is "defines (an intuitive) map from the Cartesian product of two sets vs. not so." Another equivalent solution is "columns (or rows) illustrate a consistent set of one-input operations." It is always possible to imagine the columns as inputs and the rows as operations and vice versa.
Left examples are a generalized version of the analogy structures seen in BP361. Any typical visual analogy a : b :: c : d shown in a 2x2 grid will fit on the left of this Problem.
This is a "teach" Problem (left-BP858); with many more examples it could be used to nonverbally teach this structure to somebody, similarly to BP968.
All examples show grids of squares with an image in each square, such that there is some "rule" the images within the grid obey. The "rule" can be about how the images relate to their neighbors, it can involve the position of the images in the grid, and it can involve properties of the grid considered as a whole.
There is a trivial way in which any example can be parsed so that it fits on the left side: imagine each column is assigned the list of all the squares in that column and each row is assigned its number counting from the left. Then the rows and columns will indeed combine in a natural way to give the images shown. As such, the solution of this Problem assumes use of more natural interpretations of rules for these grids. All grids in this Problem should show a rule that is more intuitive to parse than "assign each column the list of all the squares in it and each row its number counting from the left and let a square in the grid show the respective square assigned at that place in the corresponding row." (Even just a random choice of squares is probably more intuitive than that, so one might say it is impossible for that to be the most intuitive rule.) |
|
|
EXAMPLE
|
|
| |
|
|
| |
| |
| |
|
| | |
|
|
|
COMMENTS
|
To clarify the solution with an example: on the left is an image of a grid where the first row features a square with three dots and a square with nine dots, and the second row features a square with four dots and square with sixteen dots. "Three" and "four" are assigned to the rows; "x" and "x squared" are assigned to the columns.
An equivalent solution with more mathematical jargon is "defines (an intuitive) map from the Cartesian product of two sets vs. not so." Another equivalent solution is "columns (or rows) illustrate a consistent set of one-input operations." It is always possible to imagine the columns as inputs and the rows as operations and vice versa.
Left examples are a generalized version of the analogy structures seen in BP361. Any typical visual analogy a : b :: c : d shown in a 2x2 grid will fit on the left of this Problem.
This is a "teach" Problem (left-BP858); with many more examples it could be used to nonverbally teach this structure to somebody, similarly to BP968.
All examples show grids of squares with an image in each square, such that there is some "rule" the images within the grid obey. The "rule" can be about how the images relate to their neighbors, it can involve the position of the images in the grid, and it can involve properties of the grid considered as a whole.
There is a trivial way in which any example can be parsed so that it fits on the left side: imagine each column is assigned the list of all the squares in that column and each row is assigned the list of all the squares in that row. Then the rows and columns will indeed combine in a natural way to give the images shown. As such, the solution of this Problem assumes use of more natural interpretations of rules for these grids. All grids in this Problem should show a rule that is more intuitive to parse than "assign each column the list of all the squares in it and each row the list of all the squares in it and let a square in the grid show the respective square assigned at that place in the corresponding column and row." (Even just a random choice of squares is more intuitive than that, so one might say it is impossible for that to be the most intuitive rule.) |
|
|
EXAMPLE
|
|
| |
|
|
| |
| |
| |
|
| | |
|
|
|
COMMENTS
|
To clarify the solution with an example: on the left is an image of a grid where the first row features a square with three dots and a square with nine dots, and the second row features a square with four dots and square with sixteen dots. "Three" and "four" are assigned to the rows; "x" and "x squared" are assigned to the columns.
An equivalent solution with more mathematical jargon is "defines (an intuitive) map from the Cartesian product of two sets vs. not so." Another equivalent solution is "columns (or rows) illustrate a consistent set of one-input operations." It is always possible to imagine the columns as inputs and the rows as operations and vice versa.
Left examples are a generalized version of the analogy structures seen in BP361. Any typical visual analogy a : b :: c : d shown in a 2x2 grid will fit on the left of this Problem.
This is a "teach" Problem (left-BP858); with many more examples it could be used to nonverbally teach this structure to somebody, similarly to BP968.
All examples show grids of squares with an image in each square, such that there is some "rule" the images within the grid obey. The "rule" can be about how the images relate to their neighbors, it can involve the position of the images in the grid, and it can involve properties of the grid considered as a whole.
There is a trivial way in which any example can be parsed so that it fits on the left side: imagine each column is assigned the list of all the squares in that column and each row is assigned the list of all the squares in that row. Then the rows and columns will indeed combine in a natural way to give the images shown. As such, the solution of this Problem assumes use of more natural interpretations of rules for these grids. All grids in this Problem should show a rule that is more intuitive to parse than "assign each column the list of all the squares in it and each row the list of all the squares in it and let a square in the grid show the respective square assigned at that place in the corresponding column and row." (Even just a random choice of squares is probably more intuitive than that, so let us say it is impossible for that to be the most intuitive rule.) |
|
|
EXAMPLE
|
|
| |
|
|
| |
| |
| |
|
| | |
|
|
|
COMMENTS
|
To clarify the solution with an example: on the left is an image of a grid where the first row features a square with three dots and a square with nine dots, and the second row features a square with four dots and square with sixteen dots. "Three" and "four" are assigned to the rows; "x" and "x squared" are assigned to the columns.
An equivalent solution with more mathematical jargon is "defines (an intuitive) map from the Cartesian product of two sets vs. not so." Another equivalent solution is "columns (or rows) illustrate a consistent set of one-input operations." It is always possible to imagine the columns as inputs and the rows as operations and vice versa.
Left examples are a generalized version of the analogy structures seen in BP361. Any typical visual analogy a : b :: c : d shown in a 2x2 grid will fit on the left of this Problem.
This is a "teach" Problem (left-BP858); with many more examples it could be used to nonverbally teach this structure to somebody, similarly to BP968.
All examples show grids of squares with an image in each square, such that there is some "rule" the images within the grid obey. The "rule" can be about how the images relate to their neighbors, it can involve the position of the images in the grid, and it can involve properties of the grid considered as a whole.
There is a trivial way in which any example can be parsed so that it fits on the left side: imagine each column is assigned the list of all the squares in that column and each row is assigned the list of all the squares in that row. Then the rows and columns will indeed combine in a natural way to give the images shown. As such, the solution of this Problem assumes use of more natural interpretations of rules for these grids. All grids in this Problem should show a rule that is more intuitive to parse than "assign each column the list of all the squares in it and each row the list of all the squares in it and let a square in the grid show the respective square assigned at that place in the corresponding column and row." (Even just a random choice of squares is probably more intuitive than that, so maybe it is impossible for that to be the most intuitive rule.) |
|
|
EXAMPLE
|
|
| |
|
|
| |
| |
| |
|
| | |
|
|
|
COMMENTS
|
To clarify the solution with an example: on the left is an image of a grid where the first row features a square with three dots and a square with nine dots, and the second row features a square with four dots and square with sixteen dots. "Three" and "four" are assigned to the rows; "x" and "x squared" are assigned to the columns.
An equivalent solution with more mathematical jargon is "defines (an intuitive) map from the cartesian product of two sets vs. not so." Another equivalent solution is "columns (or rows) illustrate a consistent set of one-input operations." It is always possible to imagine the columns as inputs and the rows as operations and vice versa.
Left examples are a generalized version of the analogy structures seen in BP361. Any typical visual analogy a : b :: c : d shown in a 2x2 grid will fit on the left of this Problem.
This is a "teach" Problem (left-BP858); with many more examples it could be used to nonverbally teach this structure to somebody, similarly to BP968.
All examples show grids of squares with an image in each square, such that there is some "rule" the images within the grid obey. The "rule" can be about how the images relate to their neighbors, it can involve the position of the images in the grid, and it can involve properties of the grid considered as a whole.
There is a trivial way in which any example can be parsed so that it fits on the left side: imagine each column is assigned the list of all the squares in that column and each row is assigned the list of all the squares in that row. Then the rows and columns will indeed combine in a natural way to give the images shown. As such, the solution of this Problem assumes use of more natural interpretations of rules for these grids. All grids in this Problem should show a rule that is more intuitive to parse than "assign each column the list of all the squares in it and each row the list of all the squares in it and let a square in the grid show the respective square assigned at that place in the corresponding column and row." (Even just a random choice of squares is probably more intuitive than that, so maybe it is impossible for that to be the most intuitive rule.) |
|
|
EXAMPLE
|
|
| |
|
|