This page is a work in progress.

A Bongard's Dozen includes

• a Bongard Problem and
• an un-sorted box.

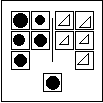
Fig. 1: Eleven boxes in this Bongard's Dozen.

In a typical Bongard's Dozen, the extra box will fit best either on the left or on the right side. You might ask someone to sort the extra box to test whether they know the answer to the Bongard Problem (without requiring them to talk about the solution in language).

There are two ways a Bongard Problem can clearly sort a specific box.

Fits on the left.

                     

Fits on the right.

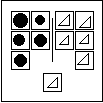
When neither of these is clear, the situation is ambiguous.

There are many reasons somebody might have trouble choosing which side of a Bongard Problem a box fits on. A common reason is that the person sorting the box doesn't know the answer to the Bongard Problem. But let us focus on the other ways a situation can be ambiguous.

Types of Ambiguity

(Keep in mind there are no clear-cut boundaries between these "types of ambiguity" in this made-up list.)

Ambiguities in Multiple Solutions

It is common for a Bongard Problem to admit more than one solution.

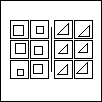
For example, the above Bongard Problem is "squares vs. triangles". But its solution could also be "squares vs. not squares" or "not triangles vs. triangles". If the two sides of a BP are not just the negations of one another, there will be multiple ways to define the threshold between the sides.
Ambiguity can result from an object not fitting cleanly into just one of the two collections.

• Fits on neither side.
  Feels like “PUSH/PUSH” (“pushed away” by both collections)
  
  

  For example, above, the wiggly black triangle is not a polygon outline, so it should go right, but it is also not a star, so it should go left.

  
  
• Fits in overlap of both sides.
  Feels like “PULL/PULL” (“pulled in” by both collections)
  
  

  For example, above, the square is a rhombus, so it should go left, but it is also a rectangle, so it should go right.
  
  Why does the solution "rhombuses vs. rectangles" seem more natural than "not rectangles vs. not rhombuses"? One point is that "being a rectangle" and "being a rhombus" are both relatively "narrow" criteria as opposed to "not being a rectangle" and "not being a rhombus".
  
  Let's say a "narrow" pattern is something a person can recognize by seeing enough examples, without needing counter-examples.
  "Is a circle" is narrow (if you see many circles together, you will think "they are circles") while "is not a circle" is not (if you see many non-circular shapes together, you will think "they are shapes").
  
  When a pattern is not narrow and its negation is narrow, call it "wide".
  "Is not a circle" is wide.
  A Bongard Problem can only communicate a wide pattern by showing the opposite narrow pattern on the other side.

• Fits on each side for independent reasons.
  Usually feels like “PUSH/PUSH”
  
  
  One side displays two distinct, narrow patterns, and the extra box fits one but not the other.
  
  
• Special case: one of these patterns has a wide (not narrow) negation shown on the other side.


• Fits that wide pattern.
  Feels like “PUSH/PUSH” (feels like the non-special cases above)
  
  


• Fits that narrow pattern.
  Feels like “PUSH/PULL” ("pulled" to wide side because we don’t register the wide property as being a requirement to fit on that side)
  
  


• The other pattern is also narrow on that side, and it too has a wide negation shown on the other side.
  
  (If this is just understood as “grey diamonds vs. not that” instead of “grey and diamond vs. neither” then the ambiguity is instead “almost fits on the positive side” described below.)


• Doesn’t quite fit on either side, but is closer to one than the other.
  Feels like “PUSH (less)/PUSH”
  
  
  Here there is an intuitive choice for where to sort the box, but it clearly doesn't quite fit.
  You could say this introduces a spectrum of closeness of fitting left versus right.

A Bongard Problem with just one solution idea (as opposed to two independent patterns) can still leave room for ambiguity.

Ambiguities on a Spectrum

• In between sides on spectrum.
       (the extra box is itself)
  
  Depending on the choice of a more specific threshold between the sides, the object could fit on either side.


• New object introduces spectrum not necessarily seen without it.
  
  
  This is clearly ambiguity whereas fitting between sides in the established spectrum is less obviously ambiguous.
  (This is arguably the same as “fits on neither side.”)


• Is both sides spliced together.
   
  (This last example is additionally plain spectrum-ambiguous if you perceive the rule as “number of concavities” instead of “wiggly outline”)


• "Spectrum Neither"
  Box falls in between sides on spectrum, but obviously fits with neither side.
  Here, the two sides of the BP may be most easily interpreted as conceptual opposites, without thinking of a spectrum; there is a gap in between the sides on the spectrum. The extra box fits in that gap.


• On precise turning-point threshold.
  


• Past one end of spectrum
  

Here there is an intuitive choice for where to sort the box, but the object doesn't quite fit. Similar to “doesn’t quite fit on either side, but is closer to one than the other.”



• Introduces new spectrum (as above)
  

Ambiguities Within a Solution Idea

• Preference of handling border case.
  
  
  The example points out there are cases which are not handled by the Bongard Problem. There may be various slightly different alternative versions of this Bongard Problem that handle border cases in various ways.


• Interpretation of the solution depends on opinion/perspective.
  
  
  Correct vs. incorrect spellings
  
  “Colour”
  
  
  This is a sign of an "invalid" culture-based Bongard Problem.


• Unclear box.
  • Extra box can't be understood in relation to problem (and it's not obvious there isn't an interpretation yet to be found that makes sense).
    
  
  
  • Answer depends on interpretation of extra box
    
    Infinite vs. 1 in number
    
    Sides of a circle
         
    Infinite vs. 0 in number
    
    Corners of a circle
         
    (In the last example we have an un-handled border case in the mini-BP.)
    
    This is very similar to "preference of handling border case". Here we are just drawing a distinction between unclear border cases that seem to be an oversight of the Bongard Problem and ambiguities that seem to be the fault of the strange extra box.
  
  
• Self-referential paradox. (Fits on a side ⇒ doesn’t fit on that side)
  
  (the extra box is itself)


• Self-referential tautology. (Fits on one side ⇒ doesn’t fit on the other)
  
  (the extra box is itself)

Other Ambiguities in One Solution

• Almost fits on the positive side where the pattern is "narrow" as described above and its negation is not.
  
  
  As above, you could say this implicitly introduces a spectrum of "closeness of fitting," but it's unclear what the threshold for fitting should be.


• Doesn’t fit in with the "world" of things shown.
  

(Calling this “ambiguity” is a stretch--the new object just expands the BP to a wider range.)

Miscellaneous "Ambiguities"

• No clear solution to problem.
  


• Clear automatic sorting despite unknown solution. (Not ambiguous.)
  


• Clear no solution to problem. (Invalid problem.)
  


• There is a clear “sorting” but in an invalid way.
  


• Some box in problem can’t be understood in context but the solution may be understandable without it.
  


• Problem seems to have error.


• Error invalidates solution, i.e. the error changes the box so it should really be on the other side.
  


• Error makes solution unclear, i.e. the error changes the box so it isn't clear where it should fit anymore.
  

This is like “some box in problem can’t be understood”



• Extra box seems to have error. (Requires much detail in box.)


• Error flips answer
  


• Error makes the answer ambiguous
  

This usually creates “unclear box” ambiguity or “fits on neither side.”



• “GoodBadBothNeither.”  Answer is “something vs. its conceptual opposite” and box fits with both.
  Feels like “PUSHPULL/PUSHPULL”
  
  People who are good vs. people who are bad
  
  Someone who has done a large bad thing and a large good thing
          
  
  Similar to “fits on both sides”, but the two properties are conceptually opposites so it also intuitively feels like the box should fit on neither side.


• Different solution interpretations give different results.
  Above were listed some types of ambiguities involving multiple solutions. Here there are multiple solutions, but people might be inclined to choose just one of them as the correct solution, and they might disagree on which one is most natural. This usually feels similar to "preference of handling border case" ambiguity. The "preference of handling border case" ambiguity is about a border case of one idea for a solution, whereas this is about multiple totally different ideas for the solution that handle a box differently. In some cases it's easy to be satisfied with a solution that handles the box and not notice there's another way of interpreting the Problem.


• Type of ambiguity depends on understanding of solution. (There are many interesting variations of this based on what ambiguities are involved.)
  
  (Plain spectrum ambiguity or spliced version of both sides depending on whether you interpret the solution as “wiggly outline” or “number of concavities”.)
  
  
  (If you interpret as rhombuses vs. rectangles it’s neither. If you interpret as two angle measures & vs. one angle measure & two side measures it’s different sides for unrelated reasons)


• Whether there is ambiguity depends on understanding of solution.
  
  (GoodBadBothNeither; “requires flip”: sorted right; “flipped vs. non-flipped”: fits in overlap; “is the flipped version”: sorted left)
  Any GoodBadBothNeither situation (see above) will admit multiple interpretations of the solution like this.
  


• Different understandings of solution sort object on different sides.
  Above example also exhibits this.


• Multiple kinds of ambiguity. (There are many variations.)
  
  (Different sides for unrelated reasons, only almost fits on left, only almost fits on right with new spectrum.)
  
  
  (Doesn’t fit in with world, splice.)
  
  
  (Spectrum, different sides for unrelated reasons one/four or less/more vs. odd/even, closer to one side than other on spectrum, arguably introduces new spectrum.)

Lastly, here are some real thinkers.