Revision history for BP934
|
|
| Displaying 1-22 of 22 results found.
|
page 1
|
|
|
Edits shown per page: 25.
|
|
|
|
|
|
| |
| |
| |
|
| | |
|
|
|
COMMENTS
|
In other words, we take the distance between points (a,b) and (c,d) to be equal to |c-a| + |d-b|, or, in other words, the distance of the shortest path between points that travels along grid lines. In mathematics, this way of measuring distance is called the 'taxicab' or 'Manhattan' metric. The points on the left hand side form equilateral triangles in this metric.
⠀
An alternate (albeit more convoluted) solution that someone may arrive at for this Problem is as follows: The triangles formed by the points on the left have some two points diagonal to each other (in the sense of bishops in chess), and considering the corresponding edge as their base, they also have an equal height. However, this was proven to be equivalent to the Manhattan distance answer by Sridhar Ramesh. Here is the proof:
⠀
An equilateral triangle amounts to points A, B, and C such that B and C lie on a circle of some radius centered at A, and the chord from B to C is as long as this radius.
A Manhattan circle of radius R is a turned square, ♢, where the Manhattan distance between any two points on opposite sides is 2R, and the Manhattan distance between any two points on adjacent sides is the larger distance from one of those points to the corner connecting those sides. Thus, to get two of these points to have Manhattan distance R, one of them must be a midpoint of one side of the ♢ (thus, bishop-diagonal from its center) and the other can then be any point on an adjacent side of the ♢ making an acute triangle with the aforementioned midpoint and center. |
|
|
EXAMPLE
|
|
| |
|
|
| |
| |
| |
|
| | |
|
|
|
COMMENTS
|
In other words, we take the distance between points (a,b) and (c,d) to be equal to |c-a| + |d-b|, or, the distance of the shortest path between points that travels along grid lines. In mathematics, this way of measuring distance is called the 'taxicab' or 'Manhattan' metric. The points on the left hand side form equilateral triangles in this metric.
⠀
An alternate (albeit more convoluted) solution that someone may arrive at for this Problem is as follows: The triangles formed by the points on the left have some two points diagonal to each other (in the sense of bishops in chess), and considering the corresponding edge as their base, they also have an equal height. However, this was proven to be equivalent to the Manhattan distance answer by Sridhar Ramesh. Here is the proof:
⠀
An equilateral triangle amounts to points A, B, and C such that B and C lie on a circle of some radius centered at A, and the chord from B to C is as long as this radius.
A Manhattan circle of radius R is a turned square, ♢, where the Manhattan distance between any two points on opposite sides is 2R, and the Manhattan distance between any two points on adjacent sides is the larger distance from one of those points to the corner connecting those sides. Thus, to get two of these points to have Manhattan distance R, one of them must be a midpoint of one side of the ♢ (thus, bishop-diagonal from its center) and the other can then be any point on an adjacent side of the ♢ making an acute triangle with the aforementioned midpoint and center. |
|
|
EXAMPLE
|
|
| |
|
|
| |
| |
| |
|
| | |
|
|
|
COMMENTS
|
In other words, we take the distance between points (a,b) and (c,d) to be equal to |c-a| + |d-b|. In mathematics, this way of measuring distance is called the 'taxicab' or 'Manhattan' metric. The points on the left hand side form equilateral triangles in this metric.
⠀
An alternate (albeit more convoluted) solution that someone may arrive at for this Problem is as follows: The triangles formed by the points on the left have some two points diagonal to each other (in the sense of bishops in chess), and considering the corresponding edge as their base, they also have an equal height. However, this was proven to be equivalent to the Manhattan distance answer by Sridhar Ramesh. Here is the proof:
⠀
An equilateral triangle amounts to points A, B, and C such that B and C lie on a circle of some radius centered at A, and the chord from B to C is as long as this radius.
A Manhattan circle of radius R is a turned square, ♢, where the Manhattan distance between any two points on opposite sides is 2R, and the Manhattan distance between any two points on adjacent sides is the larger distance from one of those points to the corner connecting those sides. Thus, to get two of these points to have Manhattan distance R, one of them must be a midpoint of one side of the ♢ (thus, bishop-diagonal from its center) and the other can then be any point on an adjacent side of the ♢ making an acute triangle with the aforementioned midpoint and center. |
|
|
EXAMPLE
|
|
| |
|
|
| |
| |
| |
|
| | |
|
|
|
COMMENTS
|
In other words, we take the distance between points (a,b) and (c,d) to be equal to |c-a| + |d-b|. In mathematics, this way of measuring distance is called the 'taxicab' or 'Manhattan' metric. The points on the left hand side form equilateral triangles in this metric.
⠀
An alternate (albeit more convoluted) solution that someone may arrive at for this Problem is as follows: The triangles formed by the points on the left have some two points diagonal to each other (in the sense of bishops in chess), and considering the corresponding edge as their base, they also have an equal height. However, this was proven to be equivalent to the Manhattan distance answer by Sridhar Ramesh. Here is the proof:
⠀
An equilateral triangle amounts to points A, B, and C such that B and C lie on a circle of some radius centered at A, and the chord from B to C is as long as this radius.
⠀
A Manhattan circle of radius R is a turned square, ♢, where the Manhattan distance between any two points on opposite sides is 2R, and the Manhattan distance between any two points on adjacent sides is the larger distance from one of those points to the corner connecting those sides. Thus, to get two of these points to have Manhattan distance R, one of them must be a midpoint of one side of the ♢ (thus, bishop-diagonal from its center) and the other can then be any point on an adjacent side of the ♢ making an acute triangle with the aforementioned midpoint and center. |
|
|
EXAMPLE
|
|
| |
|
|
| |
| |
| |
|
| | |
|
|
|
COMMENTS
|
In other words, we take the distance between points (a,b) and (c,d) to be equal to |c-a| + |d-b|. In mathematics, this way of measuring distance is called the 'taxicab' or 'Manhattan' metric. The points on the left hand side form equilateral triangles in this metric.
An alternate (albeit more convoluted) solution that someone may arrive at for this Problem is as follows: The triangles formed by the points on the left have some two points diagonal to each other (in the sense of bishops in chess), and considering the corresponding edge as their base, they also have an equal height. However, this was proven to be equivalent to the Manhattan distance answer by Sridhar Ramesh. Here is the proof:
An equilateral triangle amounts to points A, B, and C such that B and C lie on a circle of some radius centered at A, and the chord from B to C is as long as this radius.
A Manhattan circle of radius R is a turned square, ♢, where the Manhattan distance between any two points on opposite sides is 2R, and the Manhattan distance between any two points on adjacent sides is the larger distance from one of those points to the corner connecting those sides. Thus, to get two of these points to have Manhattan distance R, one of them must be a midpoint of one side of the ♢ (thus, bishop-diagonal from its center) and the other can then be any point on an adjacent side of the ♢ making an acute triangle with the aforementioned midpoint and center. |
|
|
EXAMPLE
|
|
| |
|
|
| |
| |
| |
|
| | |
|
|
|
+DATA
|
 EX7719 |
| |
|
|
| |
|
|
|
-DATA
|
 EX7720 |
| |
|
|
| |
|
|
|
REMOVE
|
 EX7711 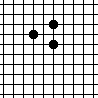 EX7713 |
| |
|
|
| |
| |
| |
|
| | |
|
|
|
NAME
|
If "distance" is taken to be the sum of horizontal and vertical distances between points, the 3 points are equidistant from each other vs. not so.
|
|
|
COMMENTS
|
In other words, we take the distance between points (a,b) and (c,d) to be equal to |c-a| + |d-b|. In mathematics, this way of measuring distance is called the 'taxicab metric'. |
|
|
EXAMPLE
|
|
|
|
AUTHOR
|
Leo Crabbe |
| |
|
|
| |
|
|
|
+DATA
|
 EX7707  EX7708  EX7709 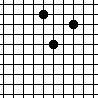 EX7710  EX7711  EX7712 |
| |
|
|
| |
|
|
|
-DATA
|
 EX7713  EX7714  EX7715  EX7716  EX7717  EX7718 |
| |
|
|
| |
| |
| |
|
| | |
|
|
|
NAME
|
|
|
|
COMMENTS
|
|
|
|
REFERENCE
|
|
|
|
CROSSREFS
|
|
|
|
EXAMPLE
|
|
|
|
AUTHOR
|
|
| |
|
|
| |
|
|
|
REMOVE
|
 EX6284  EX6285  EX6286  EX6287  EX6288  EX6289  EX6290  EX6291  EX6292  EX6294  EX6295  EX6296 |
| |
|
|
| |
| |
| |
|
| | |
|
|
|
NAME
|
|
|
|
COMMENTS
|
|
|
|
REFERENCE
|
|
|
|
CROSSREFS
|
|
|
|
EXAMPLE
|
|
|
|
AUTHOR
|
|
| |
|
|
| |
|
|
|
REMOVE
|
 EX6284  EX6285  EX6286  EX6287  EX6288  EX6289  EX6290  EX6291  EX6292  EX6294  EX6295  EX6296 |
| |
|
|
| |
| |
| |
|
| | |
|
|
|
NAME
|
|
|
|
COMMENTS
|
|
|
|
REFERENCE
|
|
|
|
CROSSREFS
|
|
|
|
EXAMPLE
|
|
|
|
AUTHOR
|
|
| |
|
|
| |
|
|
|
REMOVE
|
 EX6284  EX6285  EX6286  EX6287  EX6288  EX6289  EX6290  EX6291  EX6292  EX6294  EX6295  EX6296 |
| |
|
|
| |
| |
| |
|
| | |
|
|
|
-DATA
|
 EX6296 |
| |
|
|
| |
|
|
|
REMOVE
|
 EX6293 |
| |
|
|
| |
| |
| |
|
| | |
|
|
|
NAME
|
Ball may or may not reach edge of bounding box under gravity, depending on how strong gravity is taken to be vs. not so.
|
|
|
COMMENTS
|
|
|
|
EXAMPLE
|
|
|
|
AUTHOR
|
Leo Crabbe |
| |
|
|
| |
|
|
|
+DATA
|
 EX6284  EX6285  EX6286  EX6287  EX6288  EX6289 |
| |
|
|
| |
|
|
|
-DATA
|
 EX6290  EX6291  EX6292  EX6293  EX6294  EX6295 |
| |
|
|