Revision history for BP905
|
|
| Displaying 1-19 of 19 results found.
|
page 1
|
|
|
Edits shown per page: 25.
|
|
|
|
|
|
| |
| |
| |
|
| | |
|
|
|
-DATA
|
 EX8288 |
| |
|
|
| |
|
|
|
REMOVE
|
 EX7618 |
| |
|
|
| |
| |
| |
|
| | |
|
|
|
COMMENTS
|
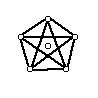
A graph is a collection of vertices and edges. Vertices are the dots and edges are the lines that connect the dots. On the left, all edges can be redrawn (curved lines are allowed and moving vertices is allowed) such that no edges cross each other and each vertex is still connected to the same other vertices. These graphs are called planar. |
|
|
EXAMPLE
|
|
| |
|
|
| |
| |
| |
|
| | |
|
|
|
COMMENTS
|
A graph is a collection of vertices and edges. Vertices are the dots and edges are the lines that connect the dots. On the left, all edges can be redrawn (curved lines are allowed) such that no edges cross each other and each vertex is still connected to the same other vertices. These graphs are called planar. |
|
|
EXAMPLE
|
|
| |
|
|
| |
| |
| |
|
| | |
|
|
|
COMMENTS
|
A graph is a collection of vertices and edges. Vertices are the dots and edges are the lines that connect the dots. On the left, all edges can be redrawn (curved lines are allowed) such that not edges cross each other and each vertex is still connected to the same other vertices. These graphs are called planar. |
|
|
EXAMPLE
|
|
| |
|
|
| |
| |
| |
|
| | |
|
|
|
NAME
|
Graph can be redrawn such that no edges intersect vs. not so.
|
|
|
COMMENTS
|
A graph is a collection of vertices and edges. Vertices are the dots and edges are the lines that connect the dots. On the left, all edges can be redrawn (curved lines are allowed) such that each vertex is still connected to the same other vertices. These graphs are called planar. |
|
|
REFERENCE
|
|
|
|
EXAMPLE
|
|
| |
|
|
| |
|
|
|
+DATA
|
 EX7612  EX7613  EX7614  EX7615  EX7616  EX7617 |
| |
|
|
| |
|
|
|
-DATA
|
 EX7618  EX7619  EX7620  EX7621  EX7622  EX7623 |
| |
|
|
| |
|
|
|
REMOVE
|
 EX7539 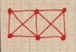 EX7540 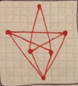 EX7541 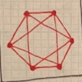 EX7542 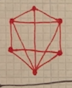 EX7543 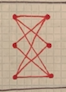 EX7544  EX7545 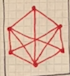 EX7546  EX7547 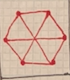 EX7548 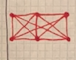 EX7549 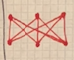 EX7550 |
| |
|
|
| |
| |
| |
|
| | |
|
|
|
COMMENTS
|
A graph is a collection of vertices and edges. Vertices are the dots and edges are the lines that connect the dots. On the left, all edges can be uncrossed while still holding the integrity of the graph, so they are all planar. On the right, not all edges can be uncrossed, so they are non-planar.
keywords: solved, +null, math, notso
concepts: graph theory, topological transformation(?), vertex of meeting lines(?), planar, crossing |
|
|
EXAMPLE
|
|
| |
|
|
| |
| |
| |
|
| | |
|
|
|
COMMENTS
|
A graph is a collection of vertices and edges. Vertices are the dots and edges are the lines that connect the dots. On the left, all edges can be uncrossed, so they are all planar. On the right, not all edges can be uncrossed, so they are non-planar.
keywords: solved, +null, math, notso
concepts: graph theory, topological transformation(?), vertex of meeting lines(?), planar, crossing |
|
|
EXAMPLE
|
|
| |
|
|
| |
| |
| |
|
| | |
|
|
|
NAME
|
planar vs non-planar
|
|
|
COMMENTS
|
A graph is a collection of vertices and edges. Vertices are the dots and edges are the lines that connect the dots. On the left, all edges can be uncrossed, so they are all planar. On the right, not all edges can be uncrossed, so they are non-planar. |
|
|
REFERENCE
|
Richard J. Trudeau, Introduction to Graph Theory, Dover Publications, 1976. |
|
|
EXAMPLE
|
|
|
|
AUTHOR
|
Molly C Klenzak |
| |
|
|
| |
|
|
|
+DATA
|
 EX7539  EX7540  EX7541  EX7542  EX7543  EX7544 |
| |
|
|
| |
|
|
|
-DATA
|
 EX7545  EX7546  EX7547  EX7548  EX7549  EX7550 |
| |
|
|
| |
| |
| |
|
| | |
|
|
|
NAME
|
|
|
|
COMMENTS
|
|
|
|
REFERENCE
|
|
|
|
CROSSREFS
|
|
|
|
EXAMPLE
|
|
|
|
AUTHOR
|
|
| |
|
|
| |
| |
| |
|
| | |
|
|
|
NAME
|
Bongard Problems with "world" small equilateral triangles, circles, and squares all the same size: some filled in black, some outlines vs. other Bongard Problems.
|
|
|
COMMENTS
|
|
|
|
EXAMPLE
|
|
|
|
AUTHOR
|
Aaron David Fairbanks |
| |
|
|