Revision history for BP898
|
|
| Displaying 1-22 of 22 results found.
|
page 1
|
|
|
Edits shown per page: 25.
|
|
|
|
|
|
| |
| |
| |
|
| | |
|
|
|
CROSSREFS
|
BP897 was conceived as a false solution for this. |
| |
|
|
| |
| |
| |
|
| | |
|
|
|
CROSSREFS
|
BP897 was conceived as an unintended solution for this. |
| |
|
|
| |
| |
| |
|
| | |
|
|
|
CROSSREFS
|
BP897 was conceived as a mistaken solution for this. |
| |
|
|
| |
| |
| |
|
| | |
|
|
|
REMOVE
|
 EX7479 |
| |
|
|
| |
| |
| |
|
| | |
|
|
|
NAME
|
Can fold into tetragonal disphenoid ("isosceles tetrahedron") vs. cannot.
|
|
|
EXAMPLE
|
|
| |
|
|
| |
| |
| |
|
| | |
|
|
|
COMMENTS
|
Which two sides are the long sides and which side is the short side, or equivalently which angles are the wider angles and which angle is the narrower angle, is the only relevant information to consider for each triangle. Triangles are all assumed isosceles and congruent to one another.
All examples in this Problem feature four of these triangles connected by corners and/or edges. |
|
|
EXAMPLE
|
|
| |
|
|
| |
| |
| |
|
| | |
|
|
|
COMMENTS
|
Which two sides are the long sides and which side is the short side, or equivalently which angles are the more obtuse angles and which angle is the more acute angle, is the only relevant information to consider for each triangle. Triangles are all assumed isosceles and congruent to one another.
All examples in this Problem feature four of these triangles connected by corners and/or edges. |
|
|
EXAMPLE
|
|
| |
|
|
| |
| |
| |
|
| | |
|
|
|
COMMENTS
|
Which two sides are the long sides and which side is the short side is the only relevant information to consider for each triangle. Triangles are all assumed isosceles and congruent to one another.
All examples in this Problem feature four isosceles triangles connected by corners and/or edges. |
|
|
EXAMPLE
|
|
| |
|
|
| |
| |
| |
|
| | |
|
|
|
COMMENTS
|
Which two sides are the long sides and which side is the short side is the only relevant information to consider for each triangle; proportions of sides and angles need not be accurate. Triangles are all assumed isosceles, congruent to one another, and to have the correct proportions.
All examples in this Problem feature four isosceles triangles connected by corners and/or edges. |
|
|
EXAMPLE
|
|
| |
|
|
| |
| |
| |
|
| | |
|
|
|
COMMENTS
|
Which two sides are the long sides and which side is the short side is the only relevant information to consider for each triangle; proportions of sides and angles need not be accurate. Triangles are all assumed isosceles, congruent to one another, and to have the correct proportions.
All examples in this Problem feature four isosceles triangles connected by corners and/or edges; were they equilateral, they would be able to be folded into a regular tetrahedron. |
|
|
EXAMPLE
|
|
| |
|
|
| |
| |
| |
|
| | |
|
|
|
COMMENTS
|
Which two sides are the long sides and which side is the short side is the only relevant information to consider for each triangle; proportions of sides and angles need not be accurate. Triangles are all assumed isosceles, congruent to one another, and to have the correct proportions.
All examples in this Problem feature four isosceles triangles connected by corners and/or edges, and, were they equilateral, they would be able to be folded into a regular tetrahedron. |
|
|
EXAMPLE
|
|
| |
|
|
| |
| |
| |
|
| | |
|
|
|
-DATA
|
 EX7485 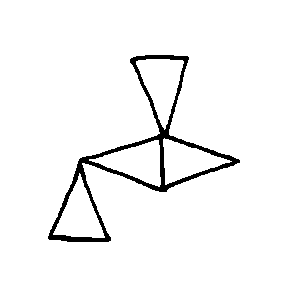 EX7486 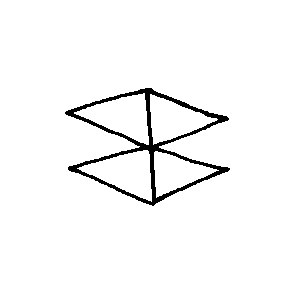 EX7487  EX7488 |
| |
|
|
| |
| |
| |
|
| | |
|
|
|
+DATA
|
 EX7473 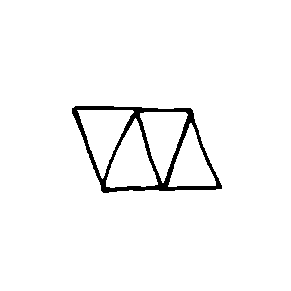 EX7474  EX7475  EX7476 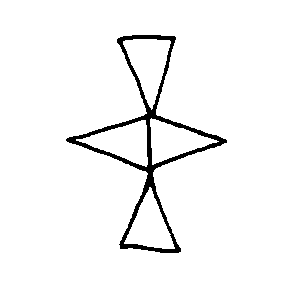 EX7477 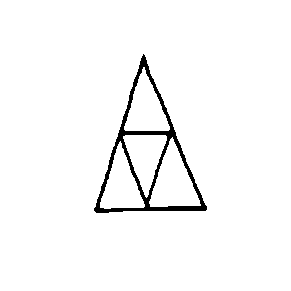 EX7478 |
| |
|
|
| |
|
|
|
-DATA
|
 EX7479 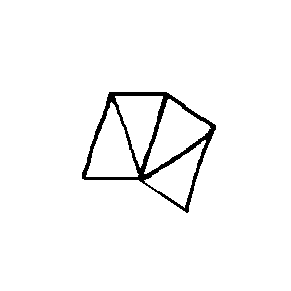 EX7480 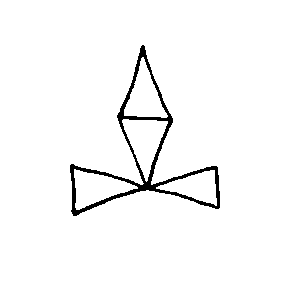 EX7481 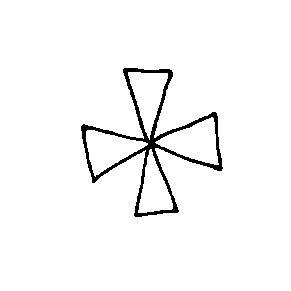 EX7482  EX7483 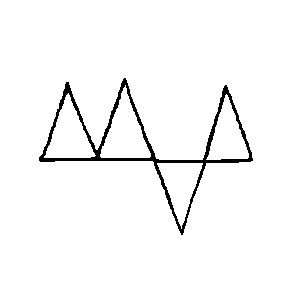 EX7484 |
| |
|
|
| |
| |
| |
|
| | |
|
|
|
NAME
|
Can fold into tetragonal disphenoid ("isosceles tetrahedron") vs cannot.
|
|
|
COMMENTS
|
Which two sides are the long sides and which side is the short side is the only relevant information to consider for each triangle; proportions of sides and angles need not be accurate. Triangles are all assumed isosceles, congruent to one another, and to have the correct proportions.
All examples in this Problem feature four triangles connected by corners and/or edges, and, were they equilateral, they would be able to be folded into a regular tetrahedron. |
|
|
EXAMPLE
|
|
|
|
AUTHOR
|
Molly C. Klenzak |
| |
|
|
| |
| |
| |
|
| | |
|
|
|
NAME
|
|
|
|
COMMENTS
|
|
|
|
REFERENCE
|
|
|
|
CROSSREFS
|
|
|
|
EXAMPLE
|
|
|
|
AUTHOR
|
|
| |
|
|
| |
| |
| |
|
| | |
|
|
|
NAME
|
Metaworld Bongard Problems for sub-worlds of shape with one hole (BP897) vs. other metaworld Bongard Problems.
|
|
|
COMMENTS
|
|
|
|
EXAMPLE
|
|
|
|
AUTHOR
|
Aaron David Fairbanks |
| |
|
|