Revision history for BP841
|
|
| Displaying 51-75 of 80 results found.
|
page 1 2 3 4
|
|
|
Edits shown per page: 25.
|
|
|
|
|
|
| |
| |
| |
|
| | |
|
|
|
COMMENTS
|
Positioning is irrelevant.
Here "relationship" is meant in the sense that one object is not allowed to be related to two distinct objects by the same relationship. "... turned 90 degrees is ..." and "... flipped horizontally is ..." are some such relationships. In all examples, any pair of objects are related to one another in a unique (most intuitive) way.
For example, in boxes on the left, if A turned 90 degrees clockwise is B, then there is an object C which is B turned 90 degrees clockwise.
Note relationships between objects can be chained. For example, if A turned 90 degrees clockwise is B, and B turned 90 degrees clockwise is C, then A turned 90 degrees then turned 90 degrees is C. Also note that if A is related to B in some way then B is related to A in some way, and the two relationships undo one another. The analogies form a mathematical group.
Drawings of collections fitting on the left (with a unique "relationship" between each two things) with relationships that will be intuitively and consistently parsed by all people in the same way are generally only possible when the relationships form an "abelian group," i.e. whenever it is true that A - - -> B, B ~~> C, and A ~~> X, it is also true that X - - -> C. (A, B, C, and X are things; - - -> and ~~> are relationships.) This is to say - - - > ~~> = ~~> - - - > for any two relationships - - -> and ~~~> that things can have. For example, rotating 10 degrees clockwise then rotating 20 degrees clockwise is the same as rotating 20 degrees then 10 degrees. However, this is not true about some relationships; rotating 10 degrees clockwise then mirroring horizontally is not the same as mirroring horizontally then rotating 10 degrees clockwise. This introduces a problem when we want to represent these relationships in this Problem. If there is one interpretation of relationships - - - >, ~~~>, and = = = > where
A - - - > B
~ ~
~ ~
V V
X = = = > C
for things A, B, C, and X, then it is likely some people might most naturally parse - - - > and = = = > as the same relationship. For example, if we have an L shape with vertical and horizontal reflections and 90 degree rotations, somebody might parse
L⅃
to be the same relationship as
┏━
┗━,
because that is L⅃ post-rotation. However, thinking in terms of performing reflections and rotations with respect to the bounding box, L⅃ is instead the same relationship as ┏━ ━┓. There will be a similar problem whenever there is a conflict between a relationship and what that relationship becomes post-[transformation]. In this example there is a conflict between "flipping with respect to the bounding box" and "flipping with respect to how L is rotated."
Sending relationships to their versions in the post-[transformation] world is more commonly called "conjugation by [transformation]." The post-[transformation] version of anything is itself for all transformations if and only if we have an abelian group.
We could decide to include non-abelian groups (and other drawings in which there is more than one choice of relationships) as examples as long as regardless of which relationships were seen the example would be sorted by the Problem the same way. We could also instead add a caveat to the solution of this Problem "there exists a choice of relationships such that..." However, these decisions may cloud the idea.
See BP842 and BP840 for versions with non-abelian groups; these Problems sidestep the problem because the solutions involve a specific way of parsing the relationships. |
|
|
EXAMPLE
|
|
| |
|
|
| |
| |
| |
|
| | |
|
|
|
COMMENTS
|
Positioning is irrelevant.
Here "relationship" is meant in the sense that one object is not allowed to be related to two distinct objects by the same relationship. "... turned 90 degrees is ..." and "... flipped horizontally is ..." are some such relationships. In all examples, any pair of objects are related to one another in a unique (most intuitive) way.
For example, in boxes on the left, if A turned 90 degrees clockwise is B, then there is an object C which is B turned 90 degrees clockwise.
Note relationships between objects can be chained. For example, if A turned 90 degrees clockwise is B, and B turned 90 degrees clockwise is C, then A turned 90 degrees then turned 90 degrees is C. Also note that if A is related to B in some way then B is related to A in some way, and the two relationships undo one another. The analogies form a mathematical group.
Drawings of collections fitting on the left (with a unique "relationship" between each two things) with a structure relationships that will be intuitively and consistently parsed by all people in the same way are generally only possible when the relationships form an "abelian group," i.e. whenever it is true that A - - -> B, B ~~> C, and A ~~> X, it is also true that X - - -> C. (A, B, C, and X are things; - - -> and ~~> are relationships.) This is to say - - - > ~~> = ~~> - - - > for any two relationships - - -> and ~~~> that things can have. For example, rotating 10 degrees clockwise then rotating 20 degrees clockwise is the same as rotating 20 degrees then 10 degrees. However, this is not true about some relationships; rotating 10 degrees clockwise then mirroring horizontally is not the same as mirroring horizontally then rotating 10 degrees clockwise. This introduces a problem when we want to represent these relationships in this Problem. If there is one interpretation of relationships - - - >, ~~~>, and = = = > where
A - - - > B
~ ~
~ ~
V V
X = = = > C
for things A, B, C, and X, then it is likely some people might most naturally parse - - - > and = = = > as the same relationship. For example, if we have an L shape with vertical and horizontal reflections and 90 degree rotations, somebody might parse
L⅃
to be the same relationship as
┏━
┗━,
because that is L⅃ post-rotation. However, thinking in terms of performing reflections and rotations with respect to the bounding box, L⅃ is instead the same relationship as ┏━ ━┓. There will be a similar problem whenever there is a conflict between a relationship and what that relationship becomes post-[transformation]. In this example there is a conflict between "flipping with respect to the bounding box" and "flipping with respect to how L is rotated."
Sending relationships to their versions in the post-[transformation] world is more commonly called "conjugation by [transformation]." The post-[transformation] version of anything is itself for all transformations if and only if we have an abelian group.
We could decide to include non-abelian groups (and other drawings in which there is more than one choice of relationships) as examples as long as regardless of which relationships were seen the example would be sorted by the Problem the same way. We could also instead add a caveat to the solution of this Problem "there exists a choice of relationships such that..." However, these decisions may cloud the idea.
See BP842 and BP840 for versions with non-abelian groups; these Problems sidestep the problem because the solutions involve a specific way of parsing the relationships. |
|
|
EXAMPLE
|
|
| |
|
|
| |
| |
| |
|
| | |
|
|
|
COMMENTS
|
Positioning is irrelevant.
Here "relationship" is meant in the sense that one object is not allowed to be related to two distinct objects by the same relationship. "... turned 90 degrees is ..." and "... flipped horizontally is ..." are some such relationships. In all examples, any pair of objects are related to one another in a unique (most intuitive) way.
For example, in boxes on the left, if A turned 90 degrees clockwise is B, then there is an object C which is B turned 90 degrees clockwise.
Note relationships between objects can be chained. For example, if A turned 90 degrees clockwise is B, and B turned 90 degrees clockwise is C, then A turned 90 degrees then turned 90 degrees is C. Also note that if A is related to B in some way then B is related to A in some way, and the two relationships undo one another. The analogies form a mathematical group.
Drawings of collections fitting on the left (with a unique "relationship" between each two things) with a structure relationships that will be intuitively and consistently parsed by all people in the same way are generally only possible when the relationships form an "abelian group," i.e. whenever it is true that A - - -> B, B ~~> C, and A ~~> X, it is also true that X - - -> C. (A, B, C, and X are things; - - -> and ~~> are relationships.) This is to say - - - > ~~> = ~~> - - - > for any two relationships - - -> and ~~~> that things can have. For example, rotating 10 degrees clockwise then rotating 20 degrees clockwise is the same as rotating 20 degrees then 10 degrees. However, this is not true about some relationships; rotating 10 degrees clockwise then mirroring horizontally is not the same as mirroring horizontally then rotating 10 degrees clockwise. This introduces a problem when we want to represent these relationships in these drawings. If there is one interpretation of relationships - - - >, ~~~>, and = = = > where
A - - - > B
~ ~
~ ~
V V
X = = = > C
for things A, B, C, and X, then it is likely some people might most naturally parse - - - > and = = = > as the same relationship. For example, if we have an L shape with vertical and horizontal reflections and 90 degree rotations, somebody might parse
L⅃
to be the same relationship as
┏━
┗━,
because that is L⅃ post-rotation. However, thinking in terms of performing reflections and rotations with respect to the bounding box, L⅃ is instead the same relationship as ┏━ ━┓. There will be a similar problem whenever there is a conflict between a relationship and what that relationship becomes post-[transformation]. In this example there is a conflict between "flipping with respect to the bounding box" and "flipping with respect to how L is rotated."
Sending relationships to their versions in the post-[transformation] world is more commonly called "conjugation by [transformation]." The post-[transformation] version of anything is itself for all transformations if and only if we have an abelian group.
We could decide to include non-abelian groups (and other drawings in which there is more than one choice of relationships) as examples as long as regardless of which relationships were seen the example would be sorted by the Problem the same way. We could also instead add a caveat to the solution of this Problem "there exists a choice of relationships such that..." However, these decisions may cloud the idea.
See BP842 and BP840 for versions with non-abelian groups; these Problems sidestep the problem because the solutions involve a specific way of parsing the relationships. |
|
|
EXAMPLE
|
|
| |
|
|
| |
| |
| |
|
| | |
|
|
|
COMMENTS
|
Positioning is irrelevant.
Here "relationship" is meant in the sense that one object is not allowed to be related to two distinct objects by the same relationship. "... turned 90 degrees is ..." and "... flipped horizontally is ..." are some such relationships. In all examples, any pair of objects are related to one another in a unique (most intuitive) way.
For example, in boxes on the left, if A turned 90 degrees clockwise is B, then there is an object C which is B turned 90 degrees clockwise.
Note relationships between objects can be chained. For example, if A turned 90 degrees clockwise is B, and B turned 90 degrees clockwise is C, then A turned 90 degrees then turned 90 degrees is C. Also note that if A is related to B in some way then B is related to A in some way, and the two relationships undo one another. The analogies form a mathematical group.
Drawings of collections fitting on the left (with a unique "relationship" between each two things) with a structure relationships that will be intuitively and consistently parsed by all people in the same way are generally only possible when the relationships form an "abelian group," i.e. whenever it is true that A - - -> B, B ~~> C, and A ~~> X, it is also true that X - - -> C. (A, B, C, and X are things; - - -> and ~~> are relationships.) This is to say - - - > ~~> = ~~> - - - > for any two relationships - - -> and ~~~> that things can have. For example, rotating 10 degrees clockwise then rotating 20 degrees clockwise is the same as rotating 20 degrees then 10 degrees. However, this is not true about some relationships; rotating 10 degrees clockwise then mirroring horizontally is not the same as mirroring horizontally then rotating 10 degrees clockwise. This introduces a problem when we want to represent these relationships in these drawings. If there is one interpretation of relationships - - - >, ~~~>, and = = = > where
A - - - > B
~ ~
~ ~
V V
X = = = > C
for things A, B, C, and X, then it is likely some people might most naturally parse - - - > and = = = > as the same relationship. For example, if we have an L shape with vertical and horizontal reflections and 90 degree rotations, somebody might parse
L⅃
to be the same relationship as
┏━
┗━,
because that is L⅃ post-rotation. However, thinking in terms of performing reflections and rotations with respect to the bounding box, L⅃ is instead the same relationship as ┏━ ━┓. There will be a similar problem whenever there is a conflict between a relationship and what that relationship becomes post-[transformation]. In this example there is a conflict between "flipping with respect to the bounding box" and "flipping with respect to how L is rotated."
Sending relationships to their versions in the post-[transformation] world is more commonly called "conjugation by [transformation]." The post-[transformation] version of anything is itself for all transformations if and only if we have an abelian group.
We could decide to include non-abelian groups (and other drawings in which there is more than one choice of relationships) as examples as long as regardless of which relationships were seen the example would be sorted by the Problem the same way. We could also instead add a caveat to the solution of this Problem "there exists a choice of relationships such that. . ." However, these decisions may cloud the idea.
See BP842 and BP840 for versions with non-abelian groups; these Problems sidestep the problem because the solutions involve a specific way of parsing the relationships. |
|
|
EXAMPLE
|
|
| |
|
|
| |
| |
| |
|
| | |
|
|
|
NAME
|
Any relationship that exists between one object and another exists between each object and some other versus not so.
|
|
|
COMMENTS
|
|
|
|
EXAMPLE
|
|
| |
|
|
| |
| |
| |
|
| | |
|
|
|
COMMENTS
|
Positioning is irrelevant.
Here "relationship" is meant in the sense that one object is not allowed to be related to two distinct objects by the same relationship. "... turned 90 degrees is ..." and "... flipped horizontally is ..." are some such relationships. In all examples, any pair of objects are related to one another in a unique (most intuitive) way.
For example, in boxes on the left, if A turned 90 degrees clockwise is B, then there is an object C which is B turned 90 degrees clockwise.
Note relationships between objects can be chained. For example, if A turned 90 degrees clockwise is B, and B turned 90 degrees clockwise is C, then A turned 90 degrees then turned 90 degrees is C. Also note that if A is related to B in some way then B is related to A in some way, and the two relationships undo one another. The analogies form a mathematical group.
Drawings of collections fitting on the left (with a unique "relationship" between each two things) with a structure relationships that will be intuitively and consistently parsed by all people in the same way are generally only possible when the relationships form an "abelian group," i.e. whenever it is true that A - - -> B, B ~~> C, and A ~~> X, it is also true that X - - -> C. (A, B, C, and X are things; - - -> and ~~> are relationships.) This is to say - - - > ~~> = ~~> - - - > for any two relationships - - -> and ~~~> that things can have. For example, rotating 10 degrees clockwise then rotating 20 degrees clockwise is the same as rotating 20 degrees then 10 degrees. However, this is not true about some relationships; rotating 10 degrees clockwise then mirroring horizontally is not the same as mirroring horizontally then rotating 10 degrees clockwise. This introduces a problem when we want to represent these relationships in these drawings. If there is one interpretation of relationships as - - - >, ~~~>, and = = = > where
A - - - > B
~ ~
~ ~
V V
X = = = > C
for things A, B, C, and X, then it is likely some people might most naturally parse - - - > and = = = > as the same relationship. For example, if we have an L shape with vertical and horizontal reflections and 90 degree rotations, somebody might parse
L⅃
to be the same relationship as
┏━
┗━,
because that is L⅃ post-rotation. However, thinking in terms of performing reflections and rotations with respect to the bounding box, L⅃ is instead the same relationship as ┏━ ━┓. There will be a similar problem whenever there is a conflict between a relationship and what that relationship becomes post-[transformation]. In this example there is a conflict between "flipping with respect to the bounding box" and "flipping with respect to how L is rotated."
Sending relationships to their versions in the post-[transformation] world is more commonly called "conjugation by [transformation]." The post-[transformation] version of anything is itself for all transformations if and only if we have an abelian group.
We could decide to include non-abelian groups (and other drawings in which there is more than one choice of relationships) as examples as long as regardless of which relationships were seen the example would be sorted by the Problem the same way. We could also instead add a caveat to the solution of this Problem "there exists a choice of relationships such that. . ." However, these decisions may cloud the idea.
See BP842 and BP840 for versions with non-abelian groups; these Problems sidestep the problem because the solutions involve a specific way of parsing the relationships. |
|
|
EXAMPLE
|
|
| |
|
|
| |
| |
| |
|
| | |
|
|
|
COMMENTS
|
Positioning is irrelevant.
Here "relationship" is meant in the sense that one object is not allowed to be related to two distinct objects by the same relationship. "... turned 90 degrees is ..." and "... flipped horizontally is ..." are some such relationships. In all examples, any pair of objects are related to one another in a unique (most intuitive) way.
For example, in boxes on the left, if A turned 90 degrees clockwise is B, then there is an object C which is B turned 90 degrees clockwise.
Note relationships between objects can be chained. For example, if A turned 90 degrees clockwise is B, and B turned 90 degrees clockwise is C, then A turned 90 degrees then turned 90 degrees is C. Also note that if A is related to B in some way then B is related to A in some way, and the two relationships undo one another. The analogies form a mathematical group.
Drawings of collections fitting on the left (with a unique "relationship" between each two things) with a structure relationships that will be intuitively and consistently parsed by all people in the same way are generally only possible when the relationships form an "abelian group," i.e. whenever it is true that A - - -> B, B ~~> C, and A ~~> X, it is also true that X - - -> C. (A, B, C, and X are things; - - -> and ~~> are relationships.) This is to say - - - > ~~> = ~~> - - - > for any two relationships - - -> and ~~~> that things can have. For example, rotating 10 degrees clockwise then rotating 20 degrees clockwise is the same as rotating 20 degrees then 10 degrees. However, this is not true about some relationships; rotating 10 degrees clockwise then mirroring horizontally is not the same as mirroring horizontally then rotating 10 degrees clockwise. This introduces a problem when we want to represent these relationships in these drawings. If there is one interpretation of relationships as - - - >, ~~~>, and = = = > where
A - - - > B
~ ~
~ ~
V V
X = = = > C
for things A, B, C, and X, then it is likely some people might most naturally parse - - - > and = = = > as the same relationship. For example, if we have an L shape with vertical and horizontal reflections and 90 degree rotations, somebody might parse
L⅃
to be the same relationship as
┏━
┗━,
because that is L⅃ post-rotation. However, thinking in terms of performing reflections and rotations with respect to the bounding box, L⅃ is instead the same relationship as ┏━ ━┓. There will be a similar problem whenever there is a conflict between a relationship and what that relationship becomes post-[transformation]. In this example there is a conflict between "flipping with respect to the bounding box" and "flipping with respect to how L is rotated."
Sending relationships to their versions in the post-[transformation] world is more commonly called "conjugation by [transformation]." The post-[transformation] version of anything is itself for all transformations if and only if we have an abelian group.
I could have decided to involve non-abelian groups (and other drawings in which there is more than one choice of relationships) as examples as long as regardless of which relationships were seen the example would be sorted by the Problem the same way. I also could have instead added a caveat to the solution of this Problem "there exists a choice of relationships such that. . ." However, these decisions may have clouded the idea.
See BP842 and BP840 for versions with non-abelian groups; these Problems sidestep the problem because the solutions involve a specific way of parsing the relationships. |
|
|
EXAMPLE
|
|
| |
|
|
| |
| |
| |
|
| | |
|
|
|
COMMENTS
|
Positioning is irrelevant.
Here "relationship" is meant in the sense that one object is not allowed to be related to two distinct objects by the same relationship. "... turned 90 degrees is ..." and "... flipped horizontally is ..." are some such relationships. In all examples, any pair of objects are related to one another in a unique (most intuitive) way.
For example, in boxes on the left, if A turned 90 degrees clockwise is B, then there is an object C which is B turned 90 degrees clockwise.
Note relationships between objects can be chained. For example, if A turned 90 degrees clockwise is B, and B turned 90 degrees clockwise is C, then A turned 90 degrees then turned 90 degrees is C. Also note that if A is related to B in some way then B is related to A in some way, and the two relationships undo one another. The analogies form a mathematical group.
Drawings of collections fitting on the left (with a unique "relationship" between each two things) with a structure relationships that will be intuitively and consistently parsed by all people in the same way are generally only possible when the relationships form an "abelian group," i.e. whenever it is true that A - - -> B, B ~~> C, and A ~~> X, it is also true that X - - -> C. (A, B, C, and X are things; - - -> and ~~> are relationships.) This is to say - - - > ~~> = ~~> - - - > for any two relationships - - -> and ~~~> that things can have. For example, rotating 10 degrees clockwise then rotating 20 degrees clockwise is the same as rotating 20 degrees then 10 degrees. However, this is not true about some relationships; rotating 10 degrees clockwise then mirroring horizontally is not the same as mirroring horizontally then rotating 10 degrees clockwise. This introduces a problem when we want to represent these relationships in these drawings. If there is one interpretation of relationships as - - - >, ~~~>, and = = = > where
A - - - > B
~ ~
~ ~
V V
X = = = > C
for things A, B, C, and X, then it is likely some people might most naturally parse - - - > and = = = > as the same relationship. For example, if we have an L shape with vertical and horizontal reflections and 90 degree rotations, somebody might parse
L⅃
to be the same relationship as
┏━
┗━,
because that is L⅃ post-rotation. However, thinking in terms of performing reflections and rotations with respect to the bounding box, L⅃ is instead the same relationship as ┏━ ━┓. There will be a similar problem whenever there is a conflict between a relationship and what that relationship becomes post-[transformation]. In this example there is a conflict between "flipping with respect to the bounding box" and "flipping with respect to how L is rotated."
Sending relationships to their versions in the post-[transformation] world is more commonly called "conjugation by [transformation]." The post-[transformation] version of anything is itself for all transformations if and only if we have an abelian group.
We could have decided to involve non-abelian groups (and other drawings in which there is more than one choice of relationships) as examples as long as regardless of which relationships were seen the example would be sorted by the Problem the same way. We also could have instead added a caveat to the solution of this Problem "there exists a choice of relationships such that. . ." However, these decisions may have clouded the idea.
See BP842 and BP840 for versions with non-abelian groups; these Problems sidestep the problem because the solutions involve a specific way of parsing the relationships. |
|
|
EXAMPLE
|
|
| |
|
|
| |
| |
| |
|
| | |
|
|
|
COMMENTS
|
Positioning is irrelevant.
Here "relationship" is meant in the sense that one object is not allowed to be related to two distinct objects by the same relationship. "... turned 90 degrees is ..." and "... flipped horizontally is ..." are some such relationships. In all examples, any pair of objects are related to one another in a unique (most intuitive) way.
For example, in boxes on the left, if A turned 90 degrees clockwise is B, then there is an object C which is B turned 90 degrees clockwise.
Note relationships between objects can be chained. For example, if A turned 90 degrees clockwise is B, and B turned 90 degrees clockwise is C, then A turned 90 degrees then turned 90 degrees is C. Also note that if A is related to B in some way then B is related to A in some way, and the two relationships undo one another. The analogies form a mathematical group.
Drawings of collections fitting on the left (with a unique "relationship" between each two things) with a structure relationships that will be intuitively and consistently parsed by all people in the same way are generally only possible when the relationships form an "abelian group," i.e. whenever it is true that A - - -> B, B ~~> C, and A ~~> X, it is also true that X - - -> C. (A, B, C, and X are things; - - -> and ~~> are relationships.) This is to say - - - > ~~> = ~~> - - - > for any two relationships - - -> and ~~~> that things can have. For example, rotating 10 degrees clockwise then rotating 20 degrees clockwise is the same as rotating 20 degrees then 10 degrees. However, this is not true about some relationships; rotating 10 degrees clockwise then mirroring horizontally is not the same as mirroring horizontally then rotating 10 degrees clockwise. This introduces a problem when we want to represent these relationships in these drawings. If there is one interpretation of relationships as - - - >, ~~~>, and = = = > where
A - - - > B
~ ~
~ ~
V V
X = = = > C
for things A, B, C, and X, then it is likely some people might most naturally parse - - - > and = = = > as the same relationship. For example, if we have an L shape with vertical and horizontal reflections and 90 degree rotations, somebody might parse
L⅃
to be the same relationship as
┏━
┗━,
because that is L⅃ post-rotation. However, thinking in terms of performing reflections and rotations with respect to the bounding box, L⅃ is instead the same relationship as ┏━ ━┓. There will be a similar problem whenever there is a conflict between a relationship and what that relationship becomes post-[transformation]. In this example there is a conflict between "flipping with respect to the bounding box" and "flipping with respect to how L is rotated."
Sending relationships to their versions in the post-[transformation] world is more commonly called "conjugation by [transformation]." The post-[transformation] version of anything is itself for all transformations if and only if we have an abelian group.
We could have decided to involve non-abelian groups (and other drawings in which there is more than one choice of relationships) as examples as long as regardless of which set of relationships were chosen the box was sorted the same. However, this may have clouded the message.
See BP842 and BP840 for versions with non-abelian groups; these Problems sidestep the problem because the solutions involve a specific way of parsing the relationships. |
|
|
EXAMPLE
|
|
| |
|
|
| |
| |
| |
|
| | |
|
|
|
COMMENTS
|
Positioning is irrelevant.
Here "relationship" is meant in the sense that one object is not allowed to be related to two distinct objects by the same relationship. "... turned 90 degrees is ..." and "... flipped horizontally is ..." are some such relationships. In all examples, any pair of objects are related to one another in a unique (most intuitive) way.
For example, in boxes on the left, if A turned 90 degrees clockwise is B, then there is an object C which is B turned 90 degrees clockwise.
Note relationships between objects can be chained. For example, if A turned 90 degrees clockwise is B, and B turned 90 degrees clockwise is C, then A turned 90 degrees then turned 90 degrees is C. Also note that if A is related to B in some way then B is related to A in some way, and the two relationships undo one another. The analogies form a mathematical group.
Drawings of collections fitting on the left (with a unique "relationship" between each two things) with a structure relationships that will be intuitively and consistently parsed by all people in the same way are generally only possible when the relationships form an "abelian group," i.e. whenever it is true that A - - -> B, B ~~> C, and A ~~> X, it is also true that X - - -> C. (A, B, C, and X are things; - - -> and ~~> are relationships.) This is to say - - - > ~~> = ~~> - - - > for any two relationships - - -> and ~~~> that things can have. For example, rotating 10 degrees clockwise then rotating 20 degrees clockwise is the same as rotating 20 degrees then 10 degrees. However, this is not true about some relationships; rotating 10 degrees clockwise then mirroring horizontally is not the same as mirroring horizontally then rotating 10 degrees clockwise. This introduces a problem when we want to represent these relationships in these drawings. If there is one interpretation of relationships as - - - >, ~~~>, and = = = > where
A - - - > B
~ ~
~ ~
V V
X = = = > C
for things A, B, C, and X, then it is likely some people might most naturally parse - - - > and = = = > as the same relationship. For example, if we have an L shape with vertical and horizontal reflections and 90 degree rotations, somebody might parse
L⅃
to be the same relationship as
┏━
┗━,
because that is L⅃ post-rotation. However, thinking in terms of performing reflections and rotations with respect to the bounding box, L⅃ is instead the same relationship as ┏━ ━┓. There will be a similar problem whenever there is a conflict between a relationship and what that relationship becomes post-[transformation]. In this example there is a conflict between "flipping with respect to the bounding box" and "flipping with respect to how L is rotated."
Sending relationships to their versions in the post-[transformation] world is more commonly called "conjugation by [transformation]." The post-[transformation] version of anything is itself for all transformations if and only if we have an abelian group.
See BP842 and BP840 for versions with non-abelian groups; these Problems sidestep the problem because the solutions involve a specific way of parsing the relationships. |
|
|
EXAMPLE
|
|
| |
|
|
| |
| |
| |
|
| | |
|
|
|
+DATA
|
 EX6963  EX6964  EX6965  EX6966 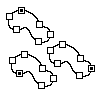 EX6967  EX6968 |
| |
|
|
| |
|
|
|
-DATA
|
 EX6969  EX6970 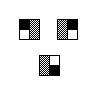 EX6971 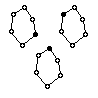 EX6972  EX6973  EX6974 |
| |
|
|
| |
| |
| |
|
| | |
|
|
|
COMMENTS
|
Positioning is irrelevant.
Here "relationship" is meant in the sense that one object is not allowed to be related to two distinct objects by the same relationship. "Turned 90 degrees is" and "flipped horizontally is" are some such relationships. Furthermore any pair of objects are related to one another in a unique (most intuitive) way.
For example, in boxes on the left, if A turned 90 degrees clockwise is B, then there is an object C which is B turned 90 degrees clockwise.
Note relationships between objects can be chained. For example, if A turned 90 degrees clockwise is B, and B turned 90 degrees clockwise is C, then A turned 90 degrees then turned 90 degrees is C. Also note that if A is related to B in some way then B is related to A in some way, and the two relationships undo one another. The analogies form a mathematical group.
Drawings of collections fitting on the left (with a unique "relationship" between each two things) with a structure relationships that will be intuitively and consistently parsed by all people in the same way are generally only possible when the relationships form an "abelian group," i.e. whenever it is true that A - - -> B, B ~~> C, and A ~~> X, it is also true that X - - -> C. (A, B, C, and X are things; - - -> and ~~> are relationships.) This is to say - - - > ~~> = ~~> - - - > for any two relationships - - -> and ~~~> that things can have. For example, rotating 10 degrees clockwise then rotating 20 degrees clockwise is the same as rotating 20 degrees then 10 degrees. However, this is not true about some relationships; rotating 10 degrees clockwise then mirroring horizontally is not the same as mirroring horizontally then rotating 10 degrees clockwise. This introduces a problem when we want to represent these relationships in these drawings. If there is one interpretation of relationships as - - - >, ~~~>, and = = = > where
A - - - > B
~ ~
~ ~
V V
X = = = > C
for things A, B, C, and X, then it is likely some people might most naturally parse - - - > and = = = > as the same relationship. For example, if we have an L shape with vertical and horizontal reflections and 90 degree rotations, somebody might parse
L⅃
to be the same relationship as
┏━
┗━,
because that is L⅃ post-rotation. However, thinking in terms of performing reflections and rotations with respect to the bounding box, L⅃ is instead the same relationship as ┏━ ━┓. There will be a similar problem whenever there is a conflict between a relationship and what that relationship becomes post-[transformation]. In this example there is a conflict between "flipping with respect to the bounding box" and "flipping with respect to how L is rotated."
Sending relationships to their versions in the post-[transformation] world is more commonly called "conjugation by [transformation]." The post-[transformation] version of anything is itself for all transformations if and only if we have an abelian group.
See BP842 and BP840 for versions with non-abelian groups; these Problems sidestep the problem because the solutions involve a specific way of parsing the relationships. |
|
|
EXAMPLE
|
|
| |
|
|
| |
| |
| |
|
| | |
|
|
|
COMMENTS
|
Positioning is irrelevant.
Here "relationship" is meant in the sense that one object is not allowed to be related to two distinct objects by the same relationship. "Turned 90 degrees is" and "flipped horizontally is" are some such relationships. Furthermore any pair of objects are related to one another in a unique (most intuitive) way.
For example, in boxes on the left, if A turned 90 degrees clockwise is B, then there is an object C which is B turned 90 degrees clockwise.
Note relationships between objects can be chained. For example, if A turned 90 degrees clockwise is B, and B turned 90 degrees clockwise is C, then A turned 90 degrees then turned 90 degrees is C. Also note that if A is related to B in some way then B is related to A in some way, and the two relationships undo one another. The analogies form a mathematical group.
Drawings of collections fitting on the left (with a unique "relationship" between each two things) with a structure relationships that will be intuitively and consistently parsed by all people in the same way are generally only possible when the relationships form an "abelian group," i.e. whenever it is true that A - - -> B, B ~~> C, and A ~~> X, it is also true that X - - -> C. (A, B, C, and X are things; - - -> and ~~> are relationships.) This is to say - - - > ~~> = ~~> - - - > for any two relationships - - -> and ~~~> that things can have. For example, rotating 10 degrees clockwise then rotating 20 degrees clockwise is the same as rotating 20 degrees then 10 degrees. However, this is not true about some relationships; rotating 10 degrees clockwise then mirroring horizontally is not the same as mirroring horizontally then rotating 10 degrees clockwise. This introduces a problem when we want to represent these relationships in these drawings. If there is one interpretation of relationships as - - - >, ~~~>, and = = = > where
A - - - > B
~ ~
~ ~
V V
X = = = > C
for things A, B, C, and X, then it is likely some people might most naturally parse - - - > and = = = > as the same relationship. For example, if we have an L shape with vertical and horizontal reflections and 90 degree rotations, somebody might parse
L⅃
to be the same relationship as
┏━
┗━,
because that is L⅃ post-rotation. However, thinking in terms of performing reflections and rotations with respect to the bounding box, L⅃ is instead the same relationship as ┏━ ━┓. There will be a similar problem whenever there is a conflict between a relationship and what that relationship becomes post-[transformation]. In this example there is a conflict between "flipping over the horizontal with respect to the bounding box" and "flipping over the horizontal with respect to how L is rotated."
Sending relationships to their versions in the post-[transformation] world is more commonly called "conjugation by [transformation]." The post-[transformation] version of anything is itself for all transformations if and only if we have an abelian group.
See BP842 and BP840 for versions with non-abelian groups; these Problems sidestep the problem because the solutions involve a specific way of parsing the relationships. |
|
|
EXAMPLE
|
|
| |
|
|
| |
| |
| |
|
| | |
|
|
|
COMMENTS
|
Positioning is irrelevant.
Here "relationship" is meant in the sense that one object is not allowed to be related to two distinct objects by the same relationship. "Turned 90 degrees is" and "flipped horizontally is" are some such relationships. Furthermore any pair of objects are related to one another in a unique (most intuitive) way.
For example, in boxes on the left, if A turned 90 degrees clockwise is B, then there is an object C which is B turned 90 degrees clockwise.
Note relationships between objects can be chained. For example, if A turned 90 degrees clockwise is B, and B turned 90 degrees clockwise is C, then A turned 90 degrees then turned 90 degrees is C. Also note that if A is related to B in some way then B is related to A in some way, and the two relationships undo one another. The analogies form a mathematical group.
Drawings of collections fitting on the left (with a unique "relationship" between each two things) with a structure relationships that will be intuitively and consistently parsed by all people in the same way are generally only possible when the relationships form an "abelian group," i.e. whenever it is true that A - - -> B, B ~~> C, and A ~~> X, it is also true that X - - -> C. (A, B, C, and X are things; - - -> and ~~> are relationships.) This is to say - - - > ~~> = ~~> - - - > for any two relationships - - -> and ~~~> that things can have. For example, rotating 10 degrees clockwise then rotating 20 degrees clockwise is the same as rotating 20 degrees then 10 degrees. However, this is not true about some relationships; rotating 10 degrees clockwise then mirroring horizontally is not the same as mirroring horizontally then rotating 10 degrees clockwise. This introduces a problem when we want to represent these relationships in these drawings. If there is one interpretation of relationships as - - - >, ~~~>, and = = = > where
A - - - > B
~ ~
~ ~
V V
X = = = > C
for things A, B, C, and X, then it is likely some people might most naturally parse - - - > and = = = > as the same relationship. For example, if we have an L shape with vertical and horizontal reflections and 90 degree rotations, somebody might parse
L⅃
to be the same relationship as
┏━
┗━,
because that is L⅃ post-rotation. However, thinking in terms of performing reflections and rotations with respect to the bounding box, L⅃ is instead the same relationship as ┏━ ━┓. There will be a similar problem whenever there is a conflict between a relationship and what that relationship becomes post-transformation. In this example there is a conflict between "flipping over the horizontal with respect to the bounding box" and "flipping over the horizontal with respect to how L is rotated."
Sending relationships to their versions in the post-transformation world is more commonly called "conjugation by transformation." The post-transformation version of anything is itself for all transformations if and only if we have an abelian group.
See BP842 and BP840 for versions with non-abelian groups; these Problems sidestep the problem because the solutions involve a specific way of parsing the relationships. |
|
|
EXAMPLE
|
|
| |
|
|
| |
| |
| |
|
| | |
|
|
|
COMMENTS
|
Positioning is irrelevant.
Here "relationship" is meant in the sense that one object is not allowed to be related to two distinct objects by the same relationship. "Turned 90 degrees is" and "flipped horizontally is" are some such relationships. Furthermore any pair of objects are related to one another in a unique (most intuitive) way.
For example, in boxes on the left, if A turned 90 degrees clockwise is B, then there is an object C which is B turned 90 degrees clockwise.
Note relationships between objects can be chained. For example, if A turned 90 degrees clockwise is B, and B turned 90 degrees clockwise is C, then A turned 90 degrees then turned 90 degrees is C. Also note that if A is related to B in some way then B is related to A in some way, and the two relationships undo one another. The analogies form a mathematical group.
Drawings of collections fitting on the left (with a unique "relationship" between each two things) with a structure relationships that will be intuitively and consistently parsed by all people in the same way are generally only possible when the relationships form an "abelian group," i.e. whenever it is true that A - - -> B, B ~~> C, and A ~~> X, it is also true that X - - -> C. (A, B, C, and X are things; - - -> and ~~> are relationships.) This is to say - - - > ~~> = ~~> - - - > for any two relationships - - -> and ~~~> that things can have. For example, rotating 10 degrees clockwise then rotating 20 degrees clockwise is the same as rotating 20 degrees then 10 degrees. However, this is not true about some relationships; rotating 10 degrees clockwise then mirroring horizontally is not the same as mirroring horizontally then rotating 10 degrees clockwise. This introduces a problem when we want to represent these relationships in these drawings. If there is one interpretation of relationships as - - - >, ~~~>, and = = = > where
A - - - > B
~ ~
~ ~
V V
X = = = > C
then it is likely some people might most naturally parse - - - > and = = = > as the same relationship. For example, if we have an L shape with vertical and horizontal reflections and 90 degree rotations, somebody might parse
L⅃
to be the same relationship as
┏━
┗━,
because that is L⅃ post-rotation. However, thinking in terms of performing reflections and rotations with respect to the bounding box, L⅃ is instead the same relationship as ┏━ ━┓. There will be a similar problem whenever there is a conflict between a relationship and what that relationship becomes post-transformation. In this example there is a conflict between "flipping over the horizontal with respect to the bounding box" and "flipping over the horizontal with respect to how L is rotated."
Sending relationships to their versions in the post-transformation world is more commonly called "conjugation by transformation." The post-transformation version of anything is itself for all transformations if and only if we have an abelian group.
See BP842 and BP840 for versions with non-abelian groups; these Problems sidestep the problem because the solutions involve a specific way of parsing the relationships. |
|
|
EXAMPLE
|
|
| |
|
|
| |
| |
| |
|
| | |
|
|
|
COMMENTS
|
Positioning is irrelevant.
Here "relationship" is meant in the sense that one object is not allowed to be related to two distinct objects by the same relationship. "Turned 90 degrees is" and "flipped horizontally is" are some such relationships. Furthermore any pair of objects are related to one another in a unique (most intuitive) way.
For example, in boxes on the left, if A turned 90 degrees clockwise is B, then there is an object C which is B turned 90 degrees clockwise.
Note relationships between objects can be chained. For example, if A turned 90 degrees clockwise is B, and B turned 90 degrees clockwise is C, then A turned 90 degrees then turned 90 degrees is C. Also note that if A is related to B in some way then B is related to A in some way, and the two relationships undo one another. The analogies form a mathematical group.
Drawings of collections fitting on the left (with a unique "relationship" between each two things) with a structure relationships that will be intuitively and consistently parsed by all people in the same way are generally only possible when the relationships form an "abelian group," i.e. whenever it is true that A - - -> B, B ~~> C, and A ~~> X, it is also true that X - - -> C. (A, B, C, and X are things; - - -> and ~~> are relationships.) This is to say - - - > ~~> = ~~> - - - > for any two relationships - - -> and ~~~> that things can have. For example, rotating 10 degrees clockwise then rotating 20 degrees clockwise is the same as rotating 20 degrees then 10 degrees. However, this is not true about some relationships; rotating 10 degrees clockwise then mirroring horizontally is not the same as mirroring horizontally then rotating 10 degrees clockwise. This introduces a problem when we want to represent these relationships in these drawings. If in one interpretation of relationships we have
A - - - > B
~ ~
~ ~
V V
X = = = > C
then it is likely some people might most naturally parse - - - > and = = = > as the same relationship. For example, if we have an L shape with vertical and horizontal reflections and 90 degree rotations, somebody might parse
L⅃
to be the same relationship as
┏━
┗━,
because that is L⅃ post-rotation. However, thinking in terms of performing reflections and rotations with respect to the bounding box, L⅃ is instead the same relationship as ┏━ ━┓. There will be a similar problem whenever there is a conflict between a relationship and what that relationship becomes post-transformation. In this example there is a conflict between "flipping over the horizontal with respect to the bounding box" and "flipping over the horizontal with respect to how L is rotated."
Sending relationships to their versions in the post-transformation world is more commonly called "conjugation by transformation." The post-transformation version of anything is itself for all transformations if and only if we have an abelian group.
See BP842 and BP840 for versions with non-abelian groups; these Problems sidestep the problem because the solutions involve a specific way of parsing the relationships. |
|
|
EXAMPLE
|
|
| |
|
|
| |
| |
| |
|
| | |
|
|
|
COMMENTS
|
Positioning is irrelevant.
Here "relationship" is meant in the sense that one object is not allowed to be related to two distinct objects by the same relationship. "Turned 90 degrees is" and "flipped horizontally is" are some such relationships. Furthermore any pair of objects are related to one another in a unique (most intuitive) way.
For example, in boxes on the left, if A turned 90 degrees clockwise is B, then there is an object C which is B turned 90 degrees clockwise.
Note relationships between objects can be chained. For example, if A turned 90 degrees clockwise is B, and B turned 90 degrees clockwise is C, then A turned 90 degrees then turned 90 degrees is C. Also note that if A is related to B in some way then B is related to A in some way, and the two relationships undo one another. The analogies form a mathematical group.
Drawings of collections fitting on the left (with a unique "relationship" between each two things) with a structure relationships that will be intuitively and consistently parsed by all people in the same way are generally only possible when the relationships form an "abelian group," i.e. whenever it is true that A - - -> B, B ~~> C, and A ~~> X, it is also true that X - - -> C. (A, B, C, and X are things; - - -> and ~~> are relationships.) This is to say - - - > ~~> = ~~> - - - > for any two relationships - - -> and ~~~> that things can have. For example, rotating 10 degrees clockwise then rotating 20 degrees clockwise is the same as rotating 20 degrees then 10 degrees. However, this is not true about some relationships; rotating 10 degrees clockwise then mirroring horizontally is not the same as mirroring horizontally then rotating 10 degrees clockwise. This introduces a problem when we want to represent these relationships in these drawings. If in one interpretation of relationships we have
A - - - > B
~ ~
~ ~
V V
X = = = > C
then it is likely some people might most naturally parse - - - > and = = = > as the same relationship. For example, if we have an L shape with vertical and horizontal reflections and 90 degree rotations, somebody might parse
L⅃
to be the same relationship as
┏━
┗━,
because that is L⅃ post-rotation. However, thinking in terms of performing reflections and rotations with respect to the bounding box, L⅃ is instead the same relationship as ┏━ ━┓. There will be a similar problem whenever there is a conflict between a relationship and what that relationship becomes post-transformation. In this example there is a conflict between "flipping over the horizontal with respect to the bounding box" and "flipping over the horizontal with respect to how L is rotated."
Sending relationships to their versions in the post-transformation world is more commonly called "conjugation by transformation." The post-transformation version of anything is itself for all transformations if and only if we have an abelian group.
See BP842 and BP840 for versions with non-abelian groups; these Problems sidestep the problem because those solutions are about a specific way of parsing the relationships. |
|
|
EXAMPLE
|
|
| |
|
|
| |
| |
| |
|
| | |
|
|
|
COMMENTS
|
Positioning is irrelevant.
Here "relationship" is meant in the sense that one object is not allowed to be related to two distinct objects by the same relationship. "Turned 90 degrees is" and "flipped horizontally is" are some such relationships. Furthermore any pair of objects are related to one another in a unique (most intuitive) way.
For example, in boxes on the left, if A turned 90 degrees clockwise is B, then there is an object C which is B turned 90 degrees clockwise.
Note relationships between objects can be chained. For example, if A turned 90 degrees clockwise is B, and B turned 90 degrees clockwise is C, then A turned 90 degrees then turned 90 degrees is C. Also note that if A is related to B in some way then B is related to A in some way, and the two relationships undo one another. The analogies form a mathematical group.
Drawings of collections fitting on the left (with a unique "relationship" between each two things) with a structure relationships that will be intuitively and consistently parsed by all people in the same way are generally only possible when the relationships form an "abelian group," i.e. whenever it is true that A - - -> B, B ~~> C, and A ~~> X, it is also true that X - - -> C. (A, B, C, and X are things; - - -> and ~~> are relationships.) This is to say - - - > ~~> = ~~> - - - > for any two relationships - - -> and ~~~> that things can have. For example, rotating 10 degrees clockwise then rotating 20 degrees clockwise is the same as rotating 20 degrees then 10 degrees. However, this is not true about some relationships; rotating 10 degrees clockwise then mirroring horizontally is not the same as mirroring horizontally then rotating 10 degrees clockwise. This introduces a problem when we want to represent these relationships in these drawings. If in one interpretation of relationships we have
A - - - > B
~ ~
~ ~
V V
X = = = > C
then it is likely some people might most naturally parse - - - > and = = = > as the same relationship. For example, if we have an L shape with vertical and horizontal reflections and 90 degree rotations, somebody might parse
L⅃
to be the same relationship as
┏━
┗━,
because that is the relationship of L⅃ post-rotation. However, thinking in terms of performing reflections and rotations with respect to absolute coordinates, L⅃ is instead the same as ┏━ ━┓. This will always be a problem when there is a conflict between a relationship and what that relationship becomes post-blank. In this example there is a conflict between "flipping over the horizontal with respect to the bounding box" and "flipping over the horizontal with respect to how L is rotated."
Sending relationships to their versions in the post-blank world is more commonly called "conjugation by blank." The post-transformation version of anything is itself for all transformations if and only if we have an abelian group. |
|
|
EXAMPLE
|
|
| |
|
|
| |
| |
| |
|
| | |
|
|
|
COMMENTS
|
Positioning is irrelevant.
Here "relationship" is meant in the sense that one object is not allowed to be related to two distinct objects by the same relationship. "Turned 90 degrees is" and "flipped horizontally is" are some such relationships. Furthermore any pair of objects are related to one another in a unique (most intuitive) way.
For example, in boxes on the left, if A turned 90 degrees clockwise is B, then there is an object C which is B turned 90 degrees clockwise.
Note relationships between objects can be chained. For example, if A turned 90 degrees clockwise is B, and B turned 90 degrees clockwise is C, then A turned 90 degrees then turned 90 degrees is C. Also note that if A is related to B in some way then B is related to A in some way, and the two relationships undo one another. The analogies form a mathematical group.
Drawings of collections fitting on the left (with a unique "relationship" between each two things) with a structure relationships that will be intuitively and consistently parsed by all people in the same way are generally only possible when the relationships form an "abelian group," i.e. whenever it is true that A - - -> B, B ~~> C, and A ~~> X, it is also true that X - - -> C. (A, B, C, and X are things; - - -> and ~~> are relationships.) This is to say - - - > ~~> = ~~> - - - > for any two relationships - - -> and ~~~> that things can have. For example, rotating 10 degrees clockwise then rotating 20 degrees clockwise is the same as rotating 20 degrees then 10 degrees. However, this is not true about some relationships; rotating 10 degrees clockwise then mirroring horizontally is not the same as mirroring horizontally then rotating 10 degrees clockwise. This introduces a problem when we want to represent these relationships in these drawings. If in one interpretation of relationships we have
A - - - > B
~ ~
~ ~
V V
X = = = > C
then it is likely some people might most naturally parse - - - > and = = = > as the same relationship. For example, if we have an L shape with vertical and horizontal reflections and 90 degree rotations, somebody might parse
L⅃
to be the same relationship as
┏━
┗━,
because that is the relationship of L⅃ post-rotation. However, thinking in terms of performing reflections and rotations with respect to absolute coordinates, L⅃ is instead the same as ┏━ ━┓. This will always be a problem when there is a conflict between a relationship and what that relationship becomes post-blank. In this example there is a conflict between "flipping over the horizontal with respect to the bounding box" and "flipping over the horizontal with respect to how L is rotated."
Sending relationships to their versions in the post-blank world is more commonly called "conjugation by blank." The post-transformation version of anything is itself for all transformations if and only if we have an abelian group. |
|
|
EXAMPLE
|
|
| |
|
|
| |
| |
| |
|
| | |
|
|
|
COMMENTS
|
Positioning is irrelevant.
Here "relationship" is meant in the sense that one object is not allowed to be related to two distinct objects by the same relationship. "Turned 90 degrees is" and "flipped horizontally is" are some such relationships. Furthermore any pair of objects are related to one another in a unique (most intuitive) way.
For example, in boxes on the left, if A turned 90 degrees clockwise is B, then there is an object C which is B turned 90 degrees clockwise.
Note relationships between objects can be chained. For example, if A turned 90 degrees clockwise is B, and B turned 90 degrees clockwise is C, then A turned 90 degrees then turned 90 degrees is C. Also note that if A is related to B in some way then B is related to A in some way, and the two relationships undo one another. The analogies form a mathematical group.
Drawings of collections fitting on the left (with a unique "relationship" between each two things) with a structure relationships that will be intuitively and consistently parsed by all people in the same way are generally only possible when the relationships form an "abelian group," i.e. whenever it is true that A - - -> B, B ~~> C, and A ~~> X, it is also true that X - - -> C. (A, B, C, and X are things; - - -> and ~~> are relationships.) This is to say - - - > ~~> = ~~> - - - > for any two relationships - - -> and ~~~> that things can have. For example, rotating 10 degrees clockwise then rotating 20 degrees clockwise is the same as rotating 20 degrees then 10 degrees. However, this is not true about some relationships; rotating 10 degrees clockwise then mirroring horizontally is not the same as mirroring horizontally then rotating 10 degrees clockwise. This introduces a problem when we want to represent these relationships in these drawings. If in one interpretation of relationships we have
A - - - > B
~ ~
~ ~
V V
X = = = > C
then it is likely some people might most naturally parse - - - > and = = = > as the same relationship. For example, if we have an L shape with vertical and horizontal reflections and 90 degree rotations, somebody might parse
L⅃
to be the same relationship as
┏━
┗━,
because that is the relationship of L⅃ post-rotation. However, thinking in terms of performing reflections and rotations with respect to absolute coordinates, L⅃ is instead the same as ┏━ ━┓. This will always be a problem when there is a conflict between a relationship and what that relationship becomes post-blank. In this example there is a conflict between "flipping over the horizontal with respect to the bounding box" and "flipping over the horizontal with respect to how L is rotated."
Sending relationships to their versions in the post-blank world is more commonly called "conjugation by blank." The post-transformation version of anything is itself for all transformations if and only if we have an abelian group. |
|
|
EXAMPLE
|
|
| |
|
|
| |
| |
| |
|
| | |
|
|
|
COMMENTS
|
Positioning is irrelevant.
Here "relationship" is meant in the sense that one object is not allowed to be related to two distinct objects by the same relationship. "Turned 90 degrees is" and "flipped horizontally is" are some such relationships. Furthermore any pair of objects are related to one another in a unique (most intuitive) way.
For example, in boxes on the left, if A turned 90 degrees clockwise is B, then there is an object C which is B turned 90 degrees clockwise.
Note relationships between objects can be chained. For example, if A turned 90 degrees clockwise is B, and B turned 90 degrees clockwise is C, then A turned 90 degrees then turned 90 degrees is C. Also note that if A is related to B in some way then B is related to A in some way, and the two relationships undo one another. The analogies form a mathematical group.
Drawings of collections fitting on the left (with a unique "relationship" between each two things) with a structure relationships that will be intuitively and consistently parsed by all people in the same way are generally only possible when the relationships form an "abelian group," i.e. whenever it is true that A - - -> B, B ~~> C, and A ~~> X, it is also true that X - - -> C. (A, B, C, and X are things; - - -> and ~~> are relationships.) This is to say - - - > ~~> = ~~> - - - > for any two relationships - - -> and ~~~> that things can have. For example, rotating 10 degrees clockwise then rotating 20 degrees clockwise is the same as rotating 20 degrees then 10 degrees. However, this is not true about some relationships; rotating 10 degrees clockwise then mirroring horizontally is not the same as mirroring horizontally then rotating 10 degrees clockwise. This introduces a problem when we want to represent these relationships in these drawings. If in one interpretation of relationships we have
A - - - > B
~ ~
~ ~
V V
X = = = > C
then it is likely some people might most naturally parse - - - > and = = = > as the same relationship. For example, if we have an L shape with vertical and horizontal reflections and 90 degree rotations, somebody might parse
L⅃
to be the same relationship as
┏━
┗━,
because that is the relationship of L⅃ post-rotation. However, thinking in terms of performing reflections and rotations with respect to absolute coordinates, L⅃ is instead the same as ┏━ ━┓. This will always be a problem when there is a conflict between a relationship and what that relationship becomes post-blank. In this example there is a conflict between "flipping over the horizontal with respect to the bounding box" and "flipping over the horizontal with respect to how L is rotated."
Sending relationships to their versions in the post-blank world is more commonly called "conjugation by blank." The post-transformation version of anything is itself for all transformations if and only if we have an abelian group. |
|
|
EXAMPLE
|
|
| |
|
|
| |
| |
| |
|
| | |
|
|
|
COMMENTS
|
Positioning is irrelevant.
Here "relationship" is meant in the sense that one object is not allowed to be related to two distinct objects by the same relationship. "Turned 90 degrees is" and "flipped horizontally is" are some such relationships. Furthermore any pair of objects are related to one another in a unique (most intuitive) way.
For example, in boxes on the left, if A turned 90 degrees clockwise is B, then there is an object C which is B turned 90 degrees clockwise.
Note relationships between objects can be chained. For example, if A turned 90 degrees clockwise is B, and B turned 90 degrees clockwise is C, then A turned 90 degrees then turned 90 degrees is C. Also note that if A is related to B in some way then B is related to A in some way, and the two relationships undo one another. The analogies form a mathematical group.
Drawings of collections fitting on the left (with a unique "relationship" between each two things) with a structure relationships that will be intuitively and consistently parsed by all people in the same way are generally only possible when the relationships form an "abelian group," i.e. whenever it is true that A - - -> B, B ~~> C, and A ~~> X, it is also true that X - - -> C. (A, B, C, and X are things; - - -> and ~~> are relationships.) This is to say - - - > ~~> = ~~> - - - > for any two relationships - - -> and ~~~> that things can have. For example, rotating 10 degrees clockwise then rotating 20 degrees clockwise is the same as rotating 20 degrees then 10 degrees. However, this is not true about some relationships; rotating 10 degrees clockwise then mirroring horizontally is not the same as mirroring horizontally then rotating 10 degrees clockwise. This introduces a problem when we want to represent these relationships in these drawings. If in one interpretation of relationships we have
A - - - > B
~ ~
~ ~
V V
X = = = > C
then it is likely some people might most naturally parse - - - > and = = = > as the same relationship. For example, if we have an L shape with vertical and horizontal reflections and 90 degree rotations, somebody might parse
L⅃
to be the same relationship as
┏━
┗━,
because that is the relationship of L⅃ post-rotation. However, thinking in terms of performing reflections and rotations with respect to absolute coordinates, L⅃ is instead the same as ┏━ ━┓. This will always be a problem when there is a conflict between a relationship and what that relationship becomes post-blank. In this example there is a conflict between "flipping over the horizontal with respect to the bounding box" and "flipping over the horizontal with respect to how L is rotated."
Sending relationships to their versions in the post-blank world is more commonly called "conjugation by blank." The post-transformation version of anything is itself for all transformations if and only if we have an abelian group. |
|
|
EXAMPLE
|
|
| |
|
|
| |
| |
| |
|
| | |
|
|
|
NAME
|
Any relationship that exists between one object and another holds between each object and some other versus not so.
|
|
|
COMMENTS
|
Positioning is irrelevant.
Here "relationship" is meant in the sense that one object is not allowed to be related to two distinct objects by the same relationship. "Turned 90 degrees is" and "flipped horizontally is" are some such relationships. Furthermore any pair of objects are related to one another in a unique (most intuitive) way.
For example, in boxes on the left, if A turned 90 degrees clockwise is B, then there is an object C which is B turned 90 degrees clockwise.
Note relationships between objects can be chained. For example, if A turned 90 degrees clockwise is B, and B turned 90 degrees clockwise is C, then A turned 90 degrees then turned 90 degrees is C. Also note that if A is related to B in some way then B is related to A in some way, and the two relationships undo one another. The analogies form a mathematical group. |
|
|
EXAMPLE
|
|
|
|
AUTHOR
|
Aaron David Fairbanks |
| |
|
|
| |
| |
| |
|
| | |
|
|
|
NAME
|
|
|
|
COMMENTS
|
|
|
|
REFERENCE
|
|
|
|
CROSSREFS
|
|
|
|
EXAMPLE
|
|
|
|
AUTHOR
|
|
| |
|
|