Revision history for BP840
|
|
| Displaying 1-23 of 23 results found.
|
page 1
|
|
|
Edits shown per page: 25.
|
|
|
|
|
|
| |
| |
| |
|
| | |
|
|
|
COMMENTS
|
Restriction of BP841 to these axis-aligned L-shapes.
Left examples represent subgroups of the dihedral group D4. |
| |
|
|
| |
| |
| |
|
| | |
|
|
|
COMMENTS
|
Restriction of BP841 to these axis-aligned L-shapes, making the Problem less abstract.
Left examples represent subgroups of the dihedral group D4. |
|
|
EXAMPLE
|
|
| |
|
|
| |
| |
| |
|
| | |
|
|
|
COMMENTS
|
Restriction of BP841 to these axis-aligned L-shapes, making the Problem less abstract.
Left examples represent subgroups of the dihedral 4 group. |
|
|
EXAMPLE
|
|
| |
|
|
| |
| |
| |
|
| | |
|
|
|
NAME
|
Any transformation (rotation or flip) that sends one L to another L sends each L to some other L versus not so.
|
|
|
COMMENTS
|
|
|
|
EXAMPLE
|
|
| |
|
|
| |
| |
| |
|
| | |
|
|
|
NAME
|
Any transformation (rotation or flip) that sends one L to another L sends each L to some other versus not so.
|
|
|
COMMENTS
|
|
|
|
EXAMPLE
|
|
| |
|
|
| |
| |
| |
|
| | |
|
|
|
NAME
|
Any transformation (isometry) that sends one L to another L sends each L to some other versus not so.
|
|
|
COMMENTS
|
|
|
|
EXAMPLE
|
|
| |
|
|
| |
| |
| |
|
| | |
|
|
|
NAME
|
Any transformation that sends one L to another L sends each L to some other versus not so.
|
|
|
COMMENTS
|
|
|
|
EXAMPLE
|
|
| |
|
|
| |
| |
| |
|
| | |
|
|
|
NAME
|
Any relationship that exists between one L and another L holds between each L and some other versus not so.
|
|
|
COMMENTS
|
Restriction of BP841 to these axis-aligned L-shapes, making the Problem less abstract. |
|
|
EXAMPLE
|
|
| |
|
|
| |
| |
| |
|
| | |
|
|
|
COMMENTS
|
Positioning is irrelevant.
Here "relationship" is meant in the sense that one object is not allowed to be related to two distinct objects by the same relationship. "Turned 90 degrees is" and "flipped horizontally is" are some such relationships. Furthermore any pair of objects are related to one another in a unique (most intuitive) way.
For example, in boxes on the left, if A turned 90 degrees clockwise is B, then there is an object C which is B turned 90 degrees clockwise.
Note relationships between objects can be chained. For example, if A turned 90 degrees clockwise is B, and B turned 90 degrees clockwise is C, then A turned 90 degrees then turned 90 degrees is C. Also note that if A is related to B in some way then B is related to A in some way, and the two relationships undo one another. The analogies form a mathematical group. |
|
|
EXAMPLE
|
|
| |
|
|
| |
| |
| |
|
| | |
|
|
|
COMMENTS
|
Positioning is irrelevant.
Here "relationship" is meant in the sense that one object is not allowed to be related to two distinct objects by the same relationship. "Turned 90 degrees is" and "flipped horizontally is" are some such relationships. Any pair of objects are related to one another in a unique (most intuitive) way.
For example, in boxes on the left, if A turned 90 degrees clockwise is B, then there is an object C which is B turned 90 degrees clockwise.
Note relationships between objects can be chained. For example, if A turned 90 degrees clockwise is B, and B turned 90 degrees clockwise is C, then A turned 90 degrees then turned 90 degrees is C. Also note that if A is related to B in some way then B is related to A in some way, and the two relationships undo one another. The analogies form a mathematical group. |
|
|
EXAMPLE
|
|
| |
|
|
| |
| |
| |
|
| | |
|
|
|
COMMENTS
|
Positioning is irrelevant.
Here "relationship" is meant in the sense that one object is not allowed to be related to two distinct objects by the same relationship. "turned 90 degrees is" and "flipped horizontally is" are some such relationships. Any pair of objects are related to one another in a unique (most intuitive) way.
For example, in boxes on the left, if A turned 90 degrees clockwise is B, then there is an object C which is B turned 90 degrees clockwise.
Note relationships between objects can be chained. For example, if A turned 90 degrees clockwise is B, and B turned 90 degrees clockwise is C, then A turned 90 degrees then turned 90 degrees is C. Also note that if A is related to B in some way then B is related to A in some way, and the two relationships undo one another. The analogies form a mathematical group. |
|
|
EXAMPLE
|
|
| |
|
|
| |
| |
| |
|
| | |
|
|
|
NAME
|
Any relationship that exists between one object and another holds between each object and some other versus not so.
|
|
|
COMMENTS
|
Positioning is irrelevant.
Here "relationship" is meant in the sense that one object is not allowed to be related to two distinct objects by the same relationship. "turned 90 degrees is _" and "_ flipped horizontally is" are some such relationships. Any pair of objects are related to one another in a unique (most intuitive) way.
For example, in boxes on the left, if A turned 90 degrees clockwise is B, then there is an object C which is B turned 90 degrees clockwise.
Note relationships between objects can be chained. For example, if A turned 90 degrees clockwise is B, and B turned 90 degrees clockwise is C, then A turned 90 degrees then turned 90 degrees is C. Also note that if A is related to B in some way then B is related to A in some way, and the two relationships undo one another. The analogies form a mathematical group. |
|
|
EXAMPLE
|
|
|
|
AUTHOR
|
Aaron David Fairbanks |
| |
|
|
| |
|
|
|
+DATA
|
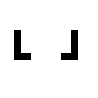 EX6939 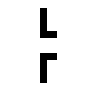 EX6940 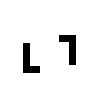 EX6941 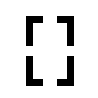 EX6942 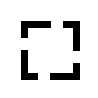 EX6943  EX6944 |
| |
|
|
| |
|
|
|
-DATA
|
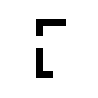 EX6945 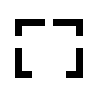 EX6946  EX6947 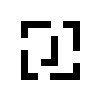 EX6948  EX6949  EX6950 |
| |
|
|
| |
| |
| |
|
| | |
|
|
|
NAME
|
|
|
|
COMMENTS
|
|
|
|
REFERENCE
|
|
|
|
CROSSREFS
|
|
|
|
EXAMPLE
|
|
|
|
AUTHOR
|
|
| |
|
|
| |
| |
| |
|
| | |
|
|
|
NAME
|
Metaworld Bongard Problems for sub-worlds of possibly self-intersecting curve (BP531) vs. other metaworld Bongard Problems.
|
|
|
COMMENTS
|
|
|
|
EXAMPLE
|
|
|
|
AUTHOR
|
Aaron David Fairbanks |
| |
|
|