Revision history for BP317
|
|
| Displaying 1-25 of 25 results found.
|
page 1
|
|
|
Edits shown per page: 25.
|
|
|
|
|
|
| |
| |
| |
|
| | |
|
|
|
COMMENTS
|
This is a Bongard Problem about comparing something discrete (number) with something continuous (size).
The inner black circles vary in size randomly. (This forces the solution to be about the discrete number of black circles instead of their combined area.) |
| |
|
|
| |
| |
| |
|
| | |
|
|
|
COMMENTS
|
This is a Bongard Problem about comparing something discrete with something continuous.
The inner black circles vary in size randomly. (This forces the solution to be about the discrete number of black circles instead of their combined area.) |
| |
|
|
| |
| |
| |
|
| | |
|
|
|
COMMENTS
|
This is a Bongard Problem about comparing something discrete with something continuous (number and size).
The inner black circles vary in size randomly. (This forces the solution to be about the discrete number of black circles instead of their combined area.) |
| |
|
|
| |
| |
| |
|
| | |
|
|
|
COMMENTS
|
This is a Bongard Problem about comparing both discrete and continuous amounts (number and size).
The inner black circles vary in size randomly. (This forces the solution to be about the discrete number of black circles instead of their combined area.) |
| |
|
|
| |
| |
| |
|
| | |
|
|
|
COMMENTS
|
This is a Bongard Problem about comparing both discrete and continuous amounts (size).
The inner black circles vary in size randomly. (This forces the solution to be about the discrete number of black circles instead of their combined area.) |
| |
|
|
| |
| |
| |
|
| | |
|
|
|
COMMENTS
|
This is a Bongard Problem about comparing discrete and continuous amounts (size).
The inner black circles vary in size randomly. (This forces the solution to be about the discrete number of black circles instead of their combined area.) |
| |
|
|
| |
| |
| |
|
| | |
|
|
|
COMMENTS
|
This is a Bongard Problem about comparing discrete with continuous amounts (size).
The inner black circles vary in size randomly. (This forces the solution to be about the discrete number of black circles instead of their combined area.) |
| |
|
|
| |
| |
| |
|
| | |
|
|
|
COMMENTS
|
This is a Bongard Problem about comparing discrete numbers with continuous amounts (size).
The inner black circles vary in size randomly. (This forces the solution to be about the discrete number of black circles instead of their combined area.) |
| |
|
|
| |
| |
| |
|
| | |
|
|
|
COMMENTS
|
This is a Bongard Problem about comparing discrete numbers with continuous amounts (size).
The inner black circles vary in size randomly. (This forces the solution to be about the number of black circles instead of their combined area.) |
| |
|
|
| |
| |
| |
|
| | |
|
|
|
COMMENTS
|
This is a Bongard Problem about comparing discrete numbers with continuous amounts (size).
The inner black circles vary in size randomly. (This is to focus the answer on the number of black circles instead of their area.) |
| |
|
|
| |
| |
| |
|
| | |
|
|
|
COMMENTS
|
This is a Bongard Problem about comparing discrete numbers with continuous amounts (size).
The inner black circles vary in size randomly. (This is to focus the answer on the number of circles instead of their area.) |
| |
|
|
| |
| |
| |
|
| | |
|
|
|
COMMENTS
|
This is a Bongard Problem about comparing discrete numbers with continuous amounts (size).
The inner black circles vary in size randomly, to show that the number of these black circles is important rather than the combined area of the black circles. |
| |
|
|
| |
| |
| |
|
| | |
|
|
|
COMMENTS
|
This is a Bongard Problem about comparing discrete numbers with continuous amounts (size). |
| |
|
|
| |
| |
| |
|
| | |
|
|
|
COMMENTS
|
This is a Bongard Problem about comparing discrete numbers with continuous quantities (size). |
| |
|
|
| |
| |
| |
|
| | |
|
|
|
COMMENTS
|
This is a Problem about comparing discrete numbers with continuous quantities (size). The size of the inner black circles varies arbitrarily, showing that the number of these black circles is what's important rather than the combined volume of the black circles. It is "necessary noise" to communicate the solution. |
|
|
EXAMPLE
|
|
| |
|
|
| |
| |
| |
|
| | |
|
|
|
COMMENTS
|
This is a Problem about comparing discrete numbers with continuous quantities (size). The size of the inner black circles varies arbitrarily, showing that the number of these black circles is what's important rather than the combined volume of the black circles. |
|
|
EXAMPLE
|
|
| |
|
|
| |
| |
| |
|
| | |
|
|
|
COMMENTS
|
This is a Problem about comparing discrete numbers with continuous spectrum-based quantities (size). The size of the inner black circles varies arbitrarily, showing that the number of these black circles is what's important rather than the combined volume of the black circles. |
|
|
EXAMPLE
|
|
| |
|
|
| |
| |
| |
|
| | |
|
|
|
COMMENTS
|
This is a Problem about comparing discrete numbers with a continuous spectrum-based quantities (size). The size of the inner black circles varies arbitrarily, showing that the number of these black circles is what's important rather than the combined volume of the black circles. |
|
|
EXAMPLE
|
|
| |
|
|
| |
| |
| |
|
| | |
|
|
|
COMMENTS
|
This is a Problem about comparing discrete numbers with a continuous spectrum-based quantities (size). The size of the inner black circles varies arbitrarily, showing that the number of these circles is what's important rather than the combined volume of the black circles. |
|
|
EXAMPLE
|
|
| |
|
|
| |
| |
| |
|
| | |
|
|
|
COMMENTS
|
This is a problem about comparing discrete numbers with a continuous spectrum-based quantities (size). The size of the inner black circles varies arbitrarily, showing that the number of these circles is what's important rather than the combined volume of the black circles. |
|
|
EXAMPLE
|
|
| |
|
|
| |
| |
| |
|
| | |
|
|
|
NAME
|
Number of enclosed black circles varies in correlation with enclosing circle outline size vs. not so.
|
|
|
COMMENTS
|
This is a problem about comparing a discrete number with a continuous spectrum-based quantity (size). The size of the inner black circles varies arbitrarily, showing that the number of these circles is what's important rather than the combined volume of the black circles. |
|
|
EXAMPLE
|
|
| |
|
|
| |
| |
| |
|
| | |
|
|
|
+DATA
|
 EX3788  EX3789  EX3790  EX3791  EX3792  EX3793 |
| |
|
|
| |
|
|
|
-DATA
|
 EX3794  EX3795  EX3796  EX3797 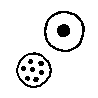 EX3798 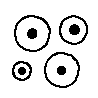 EX3799 |
| |
|
|
| |
| |
| |
|
| | |
|
|
|
NAME
|
Number of enclosed dots proportional to the circle size vs. not so.
|
|
|
COMMENTS
|
|
|
|
EXAMPLE
|
|
|
|
AUTHOR
|
Aaron David Fairbanks |
| |
|
|
| |
| |
| |
|
| | |
|
|
|
NAME
|
|
|
|
COMMENTS
|
|
|
|
REFERENCE
|
|
|
|
CROSSREFS
|
|
|
|
EXAMPLE
|
|
|
|
AUTHOR
|
|
| |
|
|