Revision history for BP1267
|
|
| Displaying 1-11 of 11 results found.
|
page 1
|
|
|
Edits shown per page: 25.
|
|
|
|
|
|
| |
| |
| |
|
| | |
|
|
|
REMOVE
|
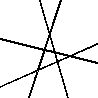 EX10137 |
| |
|
|
| |
| |
| |
|
| | |
|
|
|
+DATA
|
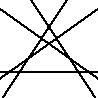 EX10167 |
| |
|
|
| |
| |
| |
|
| | |
|
|
|
COMMENTS
|
Left-sorted examples divide the plane into a maximal amount of disconnected white regions by a given number of "cuts". The number of regions in one of these examples will be the nth value of of the Lazy Caterer sequence ( https://oeis.org/A000124 ), where n is the number of lines. |
| |
|
|
| |
| |
| |
|
| | |
|
|
|
COMMENTS
|
Left-sorted examples divide the plane into a maximal amount of disconnected white regions by a given number of "cuts". The number of regions in one of these examples will be the nth value of of the Lazy Caterer sequence ( https://oeis.org/A000124 ), where n is the number of lines.
Since all of the examples given on the left have 5 lines or less, another answer is "Could be extended to a pentagram vs. not." - Aaron David Fairbanks, Oct 21 2024 |
| |
|
|
| |
| |
| |
|
| | |
|
|
|
COMMENTS
|
Left-sorted examples divide the plane into a maximal amount of disconnected white regions by a given number of "cuts". The number of regions in one of these examples will be the nth value of of the Lazy Caterer sequence (https://oeis.org/A000124), where n is the number of lines.
Since all of the examples given on the left have 5 lines or less, another answer is "Could be extended to a pentagram vs. not." - Aaron David Fairbanks, Oct 21 2024 |
| |
|
|
| |
| |
| |
|
| | |
|
|
|
COMMENTS
|
Left-sorted examples divide the plane into a maximal amount of disconnected white regions by a given number of "cuts". The number of regions in one of these examples will be the nth value of of the Lazy Caterer sequence (https://oeis.org/A000124), where n is the number of lines.
Since all of the examples on the left have 5 lines or less, another answer is "Could be extended to a pentagram vs. not." - Aaron David Fairbanks, Oct 21 2024 |
| |
|
|
| |
| |
| |
|
| | |
|
|
|
COMMENTS
|
Left-sorted examples divide the plane into a maximal amount of disconnected white regions by a given number of "cuts". The number of regions in one of these examples will be the nth value of of the Lazy Caterer sequence (https://oeis.org/A000124), where n is the number of lines.
Since all of the examples have 5 lines or less, another answer is "Could be extended to a pentagram vs. not." - Aaron David Fairbanks, Oct 21 2024 |
| |
|
|
| |
| |
| |
|
| | |
|
|
|
COMMENTS
|
Left-sorted examples divide the plane into a maximal amount of disconnected white regions by a given number of "cuts". The number of regions in one of these examples will be the nth value of of the Lazy Caterer sequence (https://oeis.org/A000124), where n is the number of lines. |
| |
|
|
| |
| |
| |
|
| | |
|
|
|
NAME
|
Any two lines intersect, and no three lines share an intersection point vs. not so.
|
|
|
COMMENTS
|
Left-sorted examples divide the plane into a maximal amount of disconnected white regions by a given number of "cuts". The number of regions in one of these examples will be the nth value of of the Lazy Caterer sequence (https://oeis.org/A000124), where n is the number of lines. |
|
|
REFERENCE
|
https://en.wikipedia.org/wiki/Lazy_caterer%27s_sequence |
|
|
AUTHOR
|
Leo Crabbe |
| |
|
|
| |
|
|
|
+DATA
|
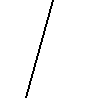 EX10132  EX10133  EX10134  EX10135 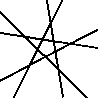 EX10136  EX10137 |
| |
|
|
| |
|
|
|
-DATA
|
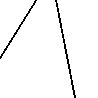 EX10138  EX10139 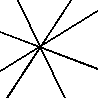 EX10140  EX10141  EX10142 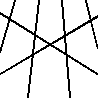 EX10143 |
| |
|
|