Revision history for BP1146
|
|
| Displaying 1-19 of 19 results found.
|
page 1
|
|
|
Edits shown per page: 25.
|
|
|
|
|
|
| |
| |
| |
|
| | |
|
|
|
COMMENTS
|
This is a difficult-to-read attempt at making a Bongard Problem about perfect numbers. Grouping columns together to make rectangular arrays, each maximal (most dots possible) rectangular array of a particular height in any given example has the same number of dots in it (a perfect number, in left-sorted cases), and the dot-width of each array represents a particular divisor of that number.
It is not currently known whether there are a finite amount of examples that would be sorted left.
Every example in this Bongard Problem corresponds to a distinct natural number. There is not a way of representing the number 1 using the rules of construction for examples in this problem (if the problem were simply "Perfect number of dots vs. other number of dots", the example with 1 dot would be sorted right). |
| |
|
|
| |
| |
| |
|
| | |
|
|
|
COMMENTS
|
This is a difficult-to-read attempt at making a Problem about perfect numbers. Grouping columns together to make rectangular arrays, each maximal (most dots possible) rectangular array of a particular height in any given example has the same number of dots in it (a perfect number, in left-sorted cases), and the dot-width of each array represents a particular divisor of that number.
It is not currently known whether there are a finite amount of examples that would be sorted left.
Every example in this Problem corresponds to a distinct natural number. There is not a way of representing the number 1 using the rules of construction for examples in this problem (if the problem were simply "Perfect number of dots vs. other number of dots", the example with 1 dot would be sorted right). |
| |
|
|
| |
| |
| |
|
| | |
|
|
|
+DATA
|
 EX9386 |
| |
|
|
| |
| |
| |
|
| | |
|
|
|
REMOVE
|
 EX9385 |
| |
|
|
| |
| |
| |
|
| | |
|
|
|
+DATA
|
 EX9385 |
| |
|
|
| |
| |
| |
|
| | |
|
|
|
COMMENTS
|
This is a difficult-to-parse attempt at making a Problem about perfect numbers. Grouping columns together to make rectangular arrays, each maximal (most dots possible) rectangular array of a particular height in any given example has the same number of dots in it (a perfect number, in left-sorted cases), and the dot-width of each array represents a particular divisor of that number.
It is not currently known whether there are a finite amount of examples that would be sorted left.
Every example in this Problem corresponds to a distinct natural number. There is not a way of representing the number 1 using the rules of construction for examples in this problem (if the problem were simply "Perfect number of dots vs. other number of dots", the example with 1 dot would be sorted right). |
| |
|
|
| |
| |
| |
|
| | |
|
|
|
COMMENTS
|
This is a difficult-to-parse attempt at making a Problem about perfect numbers. Every maximal vertical rectangular array of a particular height in any given example has the same number of dots in it (a perfect number, in left-sorted cases), and the dot-width of each array represents a particular divisor of that number.
It is not currently known whether there are a finite amount of examples that would be sorted left.
Every example in this Problem corresponds to a distinct natural number. There is not a way of representing the number 1 using the rules of construction for examples in this problem (if the problem were simply "Perfect number of dots vs. other number of dots", the example with 1 dot would be sorted right). |
| |
|
|
| |
| |
| |
|
| | |
|
|
|
+DATA
|
 EX9379  EX9380 |
| |
|
|
| |
|
|
|
-DATA
|
 EX9381  EX9382  EX9383  EX9384  EX9378 |
| |
|
|
| |
|
|
|
REMOVE
|
 EX9376 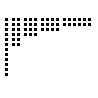 EX9374  EX9375  EX9377  EX9378 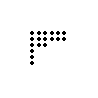 EX9371  EX9372 |
| |
|
|
| |
| |
| |
|
| | |
|
|
|
COMMENTS
|
This is a (perhaps clumsy) attempt at making a Problem about perfect numbers. Every rectangular array in any given example has the same number of dots in it (a perfect number in left-sorted cases), and the dot-width of each array represents a particular divisor of that number.
It is not currently known whether there are a finite amount of examples that would be sorted left.
Every example in this Problem corresponds to a distinct natural number. There is not a way of representing the number 1 using the rules of construction for examples in this problem (if the problem were simply "Perfect number of dots vs. other number of dots", the example with 1 dot would be sorted right). |
| |
|
|
| |
| |
| |
|
| | |
|
|
|
COMMENTS
|
This is a (perhaps clumsy) attempt at making a Problem about the perfect numbers. Every rectangular array in any given example has the same number of dots in it (a perfect number in left-sorted cases), and the dot-width of each array represents a particular divisor of that number.
It is not currently known whether there are a finite amount of examples that would be sorted left.
Every example in this Problem corresponds to a distinct natural number. There is not a way of representing the number 1 using the rules of construction for examples in this problem (if the problem were simply "Perfect number of dots vs. other number of dots", the example with 1 dot would be sorted right). |
| |
|
|
| |
| |
| |
|
| | |
|
|
|
COMMENTS
|
This is a (perhaps clumsy) attempt at making a Problem about the perfect numbers. Every rectangular array in any given left-sorted example has the same perfect number of dots in it.
It is not currently known whether there are a finite amount of examples that would be sorted left.
Every example in this Problem corresponds to a distinct natural number. There is not a way of representing the number 1 using the rules of construction for examples in this problem (if the problem were simply "Perfect number of dots vs. other number of dots", the example with 1 dot would be sorted right). |
| |
|
|
| |
| |
| |
|
| | |
|
|
|
COMMENTS
|
This is a (perhaps clumsy) attempt at making a Problem about the perfect numbers. Every rectangular array in a given left-sorted example has the same perfect number of dots in it.
It is not currently known whether there are a finite amount of examples that would be sorted left.
Every example in this Problem corresponds to a distinct natural number. There is not a way of representing the number 1 using the rules of construction for examples in this problem (if the problem were simply "Perfect number of dots vs. other number of dots", the example with 1 dot would be sorted right). |
| |
|
|
| |
| |
| |
|
| | |
|
|
|
REFERENCE
|
https://en.wikipedia.org/wiki/Perfect_number |
| |
|
|
| |
| |
| |
|
| | |
|
|
|
COMMENTS
|
This is a (perhaps clumsy) attempt at making a Problem about the perfect numbers. Every rectangular array in a given left-sorted example has the same perfect number of dots in it. It is not currently known whether there are a finite amount of examples that would be sorted left.
Every example in this Problem corresponds to a distinct natural number. There is not a way of representing the number 1 using the rules of construction for examples in this problem (if the problem were simply "Perfect number of dots vs. other number of dots", the example with 1 dot would be sorted right). |
| |
|
|
| |
| |
| |
|
| | |
|
|
|
NAME
|
Same number of dots in top row as in leftmost column vs not so.
|
|
|
COMMENTS
|
This is a (perhaps clumsy) attempt at making a Problem about the perfect numbers. Every rectangular array in a given left-sorted example has the same perfect number of dots in it. It is not known whether there are a finite amount of examples that would be sorted left.
Every example in this Problem corresponds to a distinct natural number. There is not a way of representing the number 1 using the rules of construction for examples in this problem (if the problem were simply "Perfect number of dots vs. other number of dots", the example with 1 dot would be sorted right). |
|
|
AUTHOR
|
Leo Crabbe |
| |
|
|
| |
|
|
|
+DATA
|
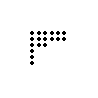 EX9371  EX9372 |
| |
|
|
| |
|
|
|
-DATA
|
 EX9373 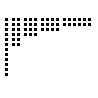 EX9374  EX9375  EX9376  EX9377  EX9378 |
| |
|
|