Revision history for BP1130
|
|
| Displaying 101-117 of 117 results found.
|
page 1 2 3 4 5
|
|
|
Edits shown per page: 25.
|
|
|
|
|
|
| |
| |
| |
|
| | |
|
|
|
COMMENTS
|
The rectangle-based description was noted by Sridhar Ramesh when he solved this.
Here is the original, more vague and instinctive description:
"Start with a string along the top path. Sweep it down, region-by-region, until it lies along the bottom path. Only in left images can this be done so that no portion of the string ever hesitates."
If a person who is trying to solve this Bongard Problem says something along these lines, they likely have the correct answer in mind. It is not so easy to make this intuition precise.
There are subtleties to this idea worth mentioning. Each point on the string can only move vertically. The string may only enter a region if the string fully covers the region's top edge (and likewise it must exit by fully covering the bottom edge). Thus a portion of string cannot enter a region until the string is finished sweeping down all the regions directly above.
This answer seems quite convoluted spelled out like this in detail. (Although it is not terribly complicated imagined visually. See the keyword "unwordable" left-BP506.)
The string-sweeping answer is equivalent to the rectangle answer because a rectangle indexes the animation of a string throughout an interval of time. (A horizontal cross-section of the rectangle represents the string, and the vertical position is time.) Distorting the rectangle into a new shape is the same as defining an animation of a string sweeping across that shape. In particular, shrinking vertical lines of the rectangle into points means just those points of the string keep stationary for some time while the string sweeps down.
Actually, all examples shown in this Bongard Problem are some form of squashed-down subdivided rectangle. The examples shown on the right of this Bongard Problem are examples that would fit left but with some whole ovals collapsed into just horizontal lines (leaving a length of string stationary in the animation). |
| |
|
|
| |
| |
| |
|
| | |
|
|
|
COMMENTS
|
The rectangle-based description was noted by Sridhar Ramesh when he solved this.
Here is the original, more vague and instinctive description:
"Start with a string along the top path. Sweep it down, region-by-region, until it lies along the bottom path. Only in left images can this be done so that no portion of the string ever hesitates."
If a person who is trying to solve this Bongard Problem says something along these lines, they likely have the correct answer in mind. It is not so easy to make this intuition precise.
There are subtleties to this idea worth mentioning. Each point on the string can only move vertically. The string may only enter a region by fully at once covering its top edge and later must exit by fully at once covering the bottom edge. Thus a portion of string cannot enter a region until the string is finished sweeping down all the regions directly above that region.
This answer seems quite convoluted spelled out like this in detail. (Although it is not terribly complicated imagined visually. See the keyword "unwordable" left-BP506.)
The string-sweeping answer is equivalent to the rectangle answer because a rectangle indexes the animation of a string throughout an interval of time. (A horizontal cross-section of the rectangle represents the string, and the vertical position is time.) Distorting the rectangle into a new shape is the same as defining an animation of a string sweeping across that shape. In particular, shrinking vertical lines of the rectangle into points means just those points of the string keep stationary for some time while the string sweeps down.
Actually, all examples shown in this Bongard Problem are some form of squashed-down subdivided rectangle. The examples shown on the right of this Bongard Problem are examples that would fit left but with some whole ovals collapsed into just horizontal lines (leaving a length of string stationary in the animation). |
|
|
CROSSREFS
|
BP1129 is an incorrect solution for this Bongard Problem. |
| |
|
|
| |
| |
| |
|
| | |
|
|
|
COMMENTS
|
The rectangle-based description was noted by Sridhar Ramesh when he solved this.
Here is the original, more vague and instinctive description:
"Start with a string along the top path. Sweep it down, region-by-region, until it lies along the bottom path. Only in left images can this be done so that no portion of the string ever hesitates."
If a person who is trying to solve this Bongard Problem says something along these lines, they likely have the correct answer in mind. It is not so easy to make this intuition precise.
There are subtleties to this idea worth mentioning. Each point on the string can only move vertically. For each region, the appropriate portion of string enters from the top edge all at the same time and reaches the bottom edge within that region all at the same time. Thus a portion of the string cannot enter a region until the string is finished sweeping down all the regions directly above that region.
This answer seems quite convoluted spelled out like this in detail. (Although it is not terribly complicated imagined visually. See the keyword "unwordable" left-BP506.)
The string-sweeping answer is equivalent to the rectangle answer because a rectangle indexes the animation of a string throughout an interval of time. (A horizontal cross-section of the rectangle represents the string, and the vertical position is time.) Distorting the rectangle into a new shape is the same as defining an animation of a string sweeping across that shape. In particular, shrinking vertical lines of the rectangle into points means just those points of the string keep stationary for some time while the string sweeps down.
Actually, all examples shown in this Bongard Problem are some form of squashed-down subdivided rectangle. The examples shown on the right of this Bongard Problem are examples that would fit left but with some whole ovals collapsed into just horizontal lines (leaving a length of string stationary in the animation). |
| |
|
|
| |
| |
| |
|
| | |
|
|
|
COMMENTS
|
The rectangle-based description was noted by Sridhar Ramesh when he solved this.
Here is the original, more vague and instinctive description:
"Start with a string along the top path. Sweep it down, region-by-region, until it lies along the bottom path. Only in left images can this be done so that no portion of the string ever hesitates."
If a person who is trying to solve this Bongard Problem says something along these lines, they likely have the correct answer in mind. It is not so easy to make this intuition precise.
There are subtleties to this idea worth mentioning. Each point on the string can only move vertically. A portion of the string moves away from the top edge within a region all at the same time and reaches the bottom edge within that region all at the same time. A portion of the string cannot enter a region until finishing sweeping down all the regions directly above that region.
This answer seems quite convoluted spelled out like this in detail. (Although it is not terribly complicated imagined visually. See the keyword "unwordable" left-BP506.)
The string-sweeping answer is equivalent to the rectangle answer because a rectangle indexes the animation of a string throughout an interval of time. (A horizontal cross-section of the rectangle represents the string, and the vertical position is time.) Distorting the rectangle into a new shape is the same as defining an animation of a string sweeping across that shape. In particular, shrinking vertical lines of the rectangle into points means just those points of the string keep stationary for some time while the string sweeps down.
Actually, all examples shown in this Bongard Problem are some form of squashed-down subdivided rectangle. The examples shown on the right of this Bongard Problem are examples that would fit left but with some whole ovals collapsed into just horizontal lines (leaving a length of string stationary in the animation). |
| |
|
|
| |
| |
| |
|
| | |
|
|
|
COMMENTS
|
The rectangle-based description was noted by Sridhar Ramesh when he solved this.
Here is the original, more vague and instinctive description:
"Start with a string along the top path. Sweep it down, region-by-region, until it lies along the bottom path. Only in left images can this be done so that no portion of the string ever hesitates."
If a person who is trying to solve this Bongard Problem says something along these lines, they likely have the correct answer in mind. It is not so easy to make this intuition precise.
There are subtleties to this idea worth mentioning. Each point on the string can only move vertically. A portion of the string moves away from the top edge within a region all at the same time and reaches the bottom edge within that region all at the same time. A portion of the string cannot move into a region until finishing sweeping down all the regions directly above it.
This answer seems quite convoluted spelled out like this in detail. (Although it is not terribly complicated imagined visually. See the keyword "unwordable" left-BP506.)
The string-sweeping answer is equivalent to the rectangle answer because a rectangle indexes the animation of a string throughout an interval of time. (A horizontal cross-section of the rectangle represents the string, and the vertical position is time.) Distorting the rectangle into a new shape is the same as defining an animation of a string sweeping across that shape. In particular, shrinking vertical lines of the rectangle into points means just those points of the string keep stationary for some time while the string sweeps down.
Actually, all examples shown in this Bongard Problem are some form of squashed-down subdivided rectangle. The examples shown on the right of this Bongard Problem are examples that would fit left but with some whole ovals collapsed into just horizontal lines (leaving a length of string stationary in the animation). |
| |
|
|
| |
| |
| |
|
| | |
|
|
|
COMMENTS
|
The rectangle-based description was noted by Sridhar Ramesh when he solved this.
Here is the original, more vague and instinctive description:
"Start with a string along the top path. Sweep it down, region-by-region, until it lies along the bottom path. Only in left images can this be done so that no portion of the string ever hesitates."
If a person who is trying to solve this Bongard Problem says something along these lines, they likely have the correct answer in mind. It is not so easy to make this intuition precise.
There are subtleties to this idea worth mentioning. The string is horizontal and can only move vertically. A portion of the string moves away from the top edge within a region all at the same time and reaches the bottom edge within that region all at the same time. A portion of the string cannot move into a region until finishing sweeping down all the regions directly above it.
This answer seems quite convoluted spelled out like this in detail. (Although it is not terribly complicated imagined visually. See the keyword "unwordable" left-BP506.)
The string-sweeping answer is equivalent to the rectangle answer because a rectangle indexes the animation of a string throughout an interval of time. (A horizontal cross-section of the rectangle represents the string, and the vertical position is time.) Distorting the rectangle into a new shape is the same as defining an animation of a string sweeping across that shape. In particular, shrinking vertical lines of the rectangle into points means just those points of the string keep stationary for some time while the string sweeps down.
Actually, all examples shown in this Bongard Problem are some form of squashed-down subdivided rectangle. The examples shown on the right of this Bongard Problem are examples that would fit left but with some whole ovals collapsed into just horizontal lines (leaving a length of string stationary in the animation). |
| |
|
|
| |
| |
| |
|
| | |
|
|
|
COMMENTS
|
The rectangle-based description was noted by Sridhar Ramesh when he solved this.
Here is the original, more vague and instinctive description:
"Start with a string along the top path. Sweep it down, region-by-region, until it lies along the bottom path. Only in left images can this be done so that no portion of the string ever hesitates."
If a person who is trying to solve this Bongard Problem says something along these lines, they likely have the correct answer in mind. It is not so easy to make this intuition precise.
There are subtleties to this idea worth addressing. The string is horizontal and can only move vertically. A portion of the string moves away from the top edge within a region all at the same time and reaches the bottom edge within that region all at the same time. A portion of the string cannot move into a region until finishing sweeping down all the regions directly above it.
This answer seems quite convoluted spelled out like this in detail. (Although it is not terribly complicated imagined visually. See the keyword "unwordable" left-BP506.)
The string-sweeping answer is equivalent to the rectangle answer because a rectangle indexes the animation of a string throughout an interval of time. (A horizontal cross-section of the rectangle represents the string, and the vertical position is time.) Distorting the rectangle into a new shape is the same as defining an animation of a string sweeping across that shape. In particular, shrinking vertical lines of the rectangle into points means just those points of the string keep stationary for some time while the string sweeps down.
Actually, all examples shown in this Bongard Problem are some form of squashed-down subdivided rectangle. The examples shown on the right of this Bongard Problem are examples that would fit left but with some whole ovals collapsed into just horizontal lines (leaving a length of string stationary in the animation). |
| |
|
|
| |
| |
| |
|
| | |
|
|
|
COMMENTS
|
The rectangle-based description was noted by Sridhar Ramesh when he solved this.
Here is the original, more vague and instinctive description:
"Start with a string along the top path. Sweep it down, region-by-region, until it lies along the bottom path. Only in left images can this be done so that no portion of the string ever hesitates."
If a person who is trying to solve this Bongard Problem says something along these lines, they likely have the correct answer in mind; the rule is just hard to get clear in words this way.
Here are some further clarifications. The string is horizontal and can only move vertically. A portion of the string moves away from the top edge within a region all at the same time and reaches the bottom edge within that region all at the same time. A portion of the string cannot move into a region until finishing sweeping down all the regions directly above it.
This answer seems quite convoluted spelled out like this in detail. (Although it is not terribly complicated imagined visually. See the keyword "unwordable" left-BP506.)
The string-sweeping answer is equivalent to the rectangle answer because a rectangle indexes the animation of a string throughout an interval of time. (A horizontal cross-section of the rectangle represents the string, and the vertical position is time.) Distorting the rectangle into a new shape is the same as defining an animation of a string sweeping across that shape. In particular, shrinking vertical lines of the rectangle into points means just those points of the string keep stationary for some time while the string sweeps down.
Actually, all examples shown in this Bongard Problem are some form of squashed-down subdivided rectangle. The examples shown on the right of this Bongard Problem are examples that would fit left but with some whole ovals collapsed into just horizontal lines (leaving a length of string stationary in the animation). |
| |
|
|
| |
| |
| |
|
| | |
|
|
|
COMMENTS
|
The rectangle-based description was noted by Sridhar Ramesh when he solved this.
This was the original, more vague and instinctive description:
"Start with a string along the top path. Sweep it down, region-by-region, until it lies along the bottom path. Only in left images can this be done so that no portion of the string ever hesitates."
If a person who is trying to solve this Bongard Problem says something along these lines, they likely have the correct answer in mind; the rule is just hard to get clear in words this way.
Here are some further clarifications. The string is horizontal and can only move vertically. A portion of the string moves away from the top edge within a region all at the same time and reaches the bottom edge within that region all at the same time. A portion of the string cannot move into a region until finishing sweeping down all the regions directly above it.
This answer seems quite convoluted spelled out like this in detail. (Although it is not terribly complicated imagined visually. See the keyword "unwordable" left-BP506.)
The string-sweeping answer is equivalent to the rectangle answer because a rectangle indexes the animation of a string throughout an interval of time. (A horizontal cross-section of the rectangle represents the string, and the vertical position is time.) Distorting the rectangle into a new shape is the same as defining an animation of a string sweeping across that shape. In particular, shrinking vertical lines of the rectangle into points means just those points of the string keep stationary for some time while the string sweeps down.
Actually, all examples shown in this Bongard Problem are some form of squashed-down subdivided rectangle. The examples shown on the right of this Bongard Problem are examples that would fit left but with some whole ovals collapsed into just horizontal lines (leaving a length of string stationary in the animation). |
| |
|
|
| |
| |
| |
|
| | |
|
|
|
NAME
|
Start with a rectangle subdivided further into rectangles and shrink the vertical lines into points vs. the shape does not result from this process.
|
| |
|
|
| |
| |
| |
|
| | |
|
|
|
NAME
|
Start with a rectangle subdivided further into rectangles and shrink the vertical lines into points vs. shape does not result from this process.
|
|
|
COMMENTS
|
The rectangle-based description was noted by Sridhar Ramesh when he solved this.
This was the original, more vague and instinctive description:
"Start with a string along the top path. Sweep it down, region-by-region, until it lies along the bottom path. Only in left images can this be done so that no portion of the string ever hesitates."
If a person who is trying to solve this Bongard Problem says something along these lines, they likely have the correct answer in mind; the rule is just hard to describe clearly this way.
Here are some clarifications. The string is horizontal and can only move vertically. A portion of the string moves away from the top edge within a region all at the same time and reaches the bottom edge within that region all at the same time. A portion of the string cannot move into a region until finishing sweeping down all the regions directly above it.
This answer seems quite convoluted spelled out like this in detail. (Although it is not terribly complicated imagined visually. See the keyword "unwordable" left-BP506.)
The string-sweeping answer is equivalent to the answer involving rectangles because a rectangle indexes the animation of a string throughout an interval of time. (A horizontal cross-section of the rectangle represents the string, and the vertical position is time.) Distorting the rectangle into a new shape is the same as defining an animation of a string sweeping across that shape. In particular, shrinking vertical lines of the rectangle into points means just those points of the string keep stationary for some time while the string sweeps down.
Actually, all examples shown in this Bongard Problem are some form of squashed-down subdivided rectangle. The examples shown on the right of this Bongard Problem are examples that would fit left but with some whole ovals collapsed into just horizontal lines (leaving a length of string stationary in the animation). |
| |
|
|
| |
| |
| |
|
| | |
|
|
|
NAME
|
Start with a rectangle subdivided further into rectangles and squish all vertical lines into points vs. shape does not result from this process.
|
|
|
COMMENTS
|
The rectangle-based description was noted by Sridhar Ramesh when he solved this.
The original description was less clear and more convoluted: "In a right example, if you start with a string along the top path and continuously morph it down into a string along the bottom path, oval-by-oval, part of the string has to hesitate somewhere." |
|
|
CROSSREFS
|
See BP1129 is a slightly different incorrect solution for this Bongard Problem. |
| |
|
|
| |
| |
| |
|
| | |
|
|
|
CROSSREFS
|
This was conceived as a false solution for BP1129. |
| |
|
|
| |
|
|
|
+DATA
|
 EX9305 |
| |
|
|
| |
|
|
|
+DATA
|
 EX9293  EX9294  EX9295 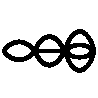 EX9296  EX9297  EX9298  EX9307  EX9308 |
| |
|
|
| |
|
|
|
-DATA
|
 EX9299  EX9300  EX9301  EX9302  EX9303  EX9304  EX9305  EX9306 |
| |
|
|