Revision history for BP213
|
|
| Displaying 1-25 of 27 results found.
|
page 1 2
|
|
|
Edits shown per page: 25.
|
|
|
|
|
|
| |
| |
| |
|
| | |
|
|
|
NAME
|
The tightest-curved section, out of all sections of curve that make a complete turn (360 degrees), contains an x-crossing point vs. not so.
|
| |
|
|
| |
| |
| |
|
| | |
|
|
|
NAME
|
The tightest-curved section, out of all continuous sections of curve that make a complete turn (360 degrees), contains an x-crossing point vs. not so.
|
| |
|
|
| |
| |
| |
|
| | |
|
|
|
NAME
|
The tightest-curved section, out of all continuous sections of curve that make a complete turn (360 degrees), contains an x-crossing point vs. not so.
|
|
|
EXAMPLE
|
|
| |
|
|
| |
| |
| |
|
| | |
|
|
|
NAME
|
Out of any continuous length of curve that makes a complete turn (360 degrees), the tightest-curved contains an x-crossing point vs. not so.
|
|
|
EXAMPLE
|
|
| |
|
|
| |
| |
| |
|
| | |
|
|
|
NAME
|
Of any section of the curve that makes a complete turn (360 degrees), the tightest-curved section contains an x-crossing point vs. not so.
|
|
|
EXAMPLE
|
|
| |
|
|
| |
| |
| |
|
| | |
|
|
|
COMMENTS
|
All examples are connected smooth curves allowed to self-intersect that must curve in only one direction (starting at one end, either clockwise or counter-clockwise), i.e. there is no inflection point. |
|
|
EXAMPLE
|
|
| |
|
|
| |
| |
| |
|
| | |
|
|
|
COMMENTS
|
All examples are connected smooth curves allowed to self-intersect that must curve in only one direction (starting at one end, either clockwise or counter-clockwise). |
|
|
EXAMPLE
|
|
| |
|
|
| |
| |
| |
|
| | |
|
|
|
COMMENTS
|
All examples are connected smooth curves allowed to self-intersect that must curve in only one direction. |
|
|
EXAMPLE
|
|
| |
|
|
| |
| |
| |
|
| | |
|
|
|
NAME
|
Of any section of the curve that makes a complete turn (360 degrees), the tightest-curved section contains an x-crossing point vs. vs. not so.
|
|
|
COMMENTS
|
|
|
|
EXAMPLE
|
|
| |
|
|
| |
| |
| |
|
| | |
|
|
|
NAME
|
Of any section of the curve that makes a complete turn (360 degrees), the tightest-curved section crosses through itself vs. vs. not so.
|
|
|
COMMENTS
|
|
|
|
EXAMPLE
|
|
| |
|
|
| |
| |
| |
|
| | |
|
|
|
NAME
|
Of any subsection of the curve that makes a complete turn (360 degrees), the tightest-curved section crosses through itself vs. vs. not so.
|
|
|
COMMENTS
|
|
|
|
EXAMPLE
|
|
| |
|
|
| |
| |
| |
|
| | |
|
|
|
NAME
|
Of any subsection of the curve that makes a complete turn (360 degrees), the tightest-curved crosses through itself vs. vs. not so.
|
|
|
COMMENTS
|
|
|
|
EXAMPLE
|
|
| |
|
|
| |
| |
| |
|
| | |
|
|
|
NAME
|
Of any subsection of the curve that makes a complete turn (360 degrees), the subsection with tightest (average) curvature crosses through itself vs. vs. not so.
|
|
|
COMMENTS
|
|
|
|
EXAMPLE
|
|
| |
|
|
| |
| |
| |
|
| | |
|
|
|
NAME
|
Out of the subsections of the curve that make a complete turn (360 degrees), the subsection with tightest (average) curvature crosses through itself vs. vs. not so.
|
|
|
COMMENTS
|
|
|
|
EXAMPLE
|
|
| |
|
|
| |
| |
| |
|
| | |
|
|
|
NAME
|
Out of any subsection of the curve that makes a complete turn (360 degrees), the subsection with tightest (average) curvature crosses through itself vs. vs. not so.
|
|
|
COMMENTS
|
|
|
|
EXAMPLE
|
|
| |
|
|
| |
| |
| |
|
| | |
|
|
|
NAME
|
Out of any section of the curve that makes a complete turn 360 degrees, the section with tightest (average) curvature crosses through itself vs. vs. not so.
|
|
|
COMMENTS
|
|
|
|
EXAMPLE
|
|
| |
|
|
| |
| |
| |
|
| | |
|
|
|
NAME
|
Out of all sections of the curve that turn 360 degrees, the one with tightest (average) curvature crosses through itself vs. vs. not so.
|
|
|
COMMENTS
|
|
|
|
EXAMPLE
|
|
| |
|
|
| |
| |
| |
|
| | |
|
|
|
NAME
|
The 360-degree arc in the curve that has the tightest (average) curvature crosses through itself vs. vs. not so.
|
|
|
COMMENTS
|
|
|
|
EXAMPLE
|
|
| |
|
|
| |
| |
| |
|
| | |
|
|
|
NAME
|
The tightest-curved section of the curve is a loop crossing through itself vs. vs. not so.
|
|
|
COMMENTS
|
|
|
|
EXAMPLE
|
|
| |
|
|
| |
| |
| |
|
| | |
|
|
|
NAME
|
There a loop crossing through itself on the generally tighter-curved end of the curve vs. not so.
|
|
|
COMMENTS
|
|
|
|
EXAMPLE
|
|
| |
|
|
| |
| |
| |
|
| | |
|
|
|
NAME
|
There a loop crossing through itself on the intuitively tighter-curved end of the curve vs. not so.
|
|
|
COMMENTS
|
|
|
|
EXAMPLE
|
|
| |
|
|
| |
| |
| |
|
| | |
|
|
|
NAME
|
Curve intersects itself near the end with greater curvature vs. not so.
|
|
|
COMMENTS
|
|
|
|
EXAMPLE
|
|
| |
|
|
| |
| |
| |
|
| | |
|
|
|
NAME
|
Curve intersects itself at the point of greatest curvature vs. not so.
|
|
|
COMMENTS
|
|
|
|
EXAMPLE
|
|
| |
|
|
| |
| |
| |
|
| | |
|
|
|
+DATA
|
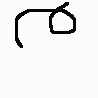 EX2540  EX2541  EX2542 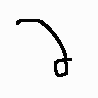 EX2543  EX2544 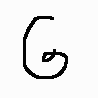 EX2545 |
| |
|
|